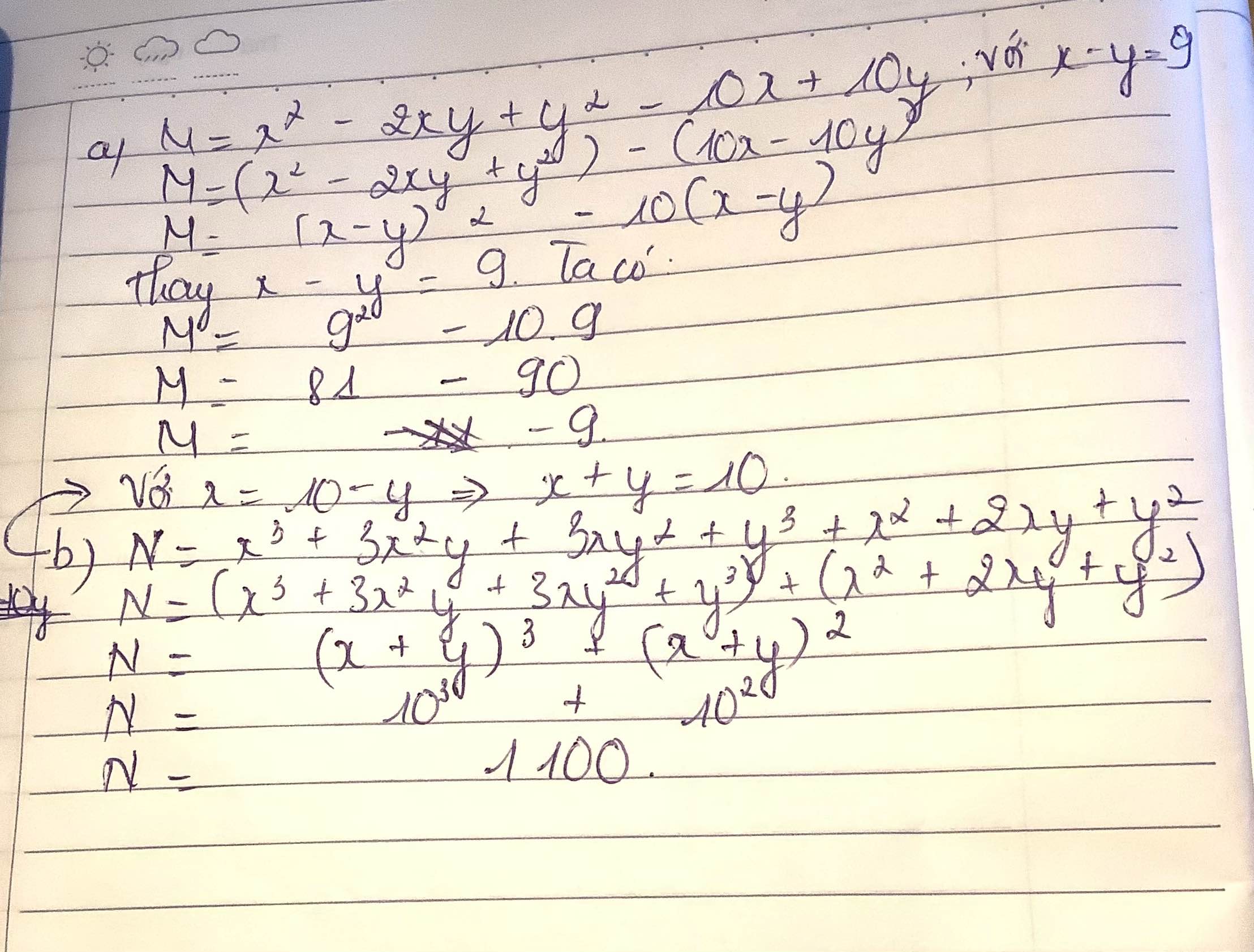Cho x+y=101. Tính: P(x,y)= x3−3x2+3x2y+3xy2+y3−3y2−6xy+3x+3y
Những câu hỏi liên quan
tính giá trị của biểu thức a) x3-3x2y+3xy2-y3 tại x=101,y=1
b)\(\dfrac{x\left(x-1\right)}{3xy^2}\)=\(\dfrac{Q}{6xy^2}\) tính Q tại x=-1
a: \(=\left(x-y\right)^3=100^3=1000000\)
Đúng 0
Bình luận (0)
c) 3x + 3y – x2 – 2xy – y2 d) x3 – x + 3x2y + 3xy2 – y + y3
c) \(3x+3y-x^2-2xy-y^2=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)d) \(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\)
\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
Đúng 3
Bình luận (0)
\(c,=3\left(x+y\right)-\left(x+y\right)^2=\left(3-x-y\right)\left(x+y\right)\\ d,=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
c) \(=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)
d) \(\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
cho x+y=5
P=3x2-2x+3y2-2y+6xy-100
Q=x3+y3-2x2-2y2+3xy(x+y)-4xy+3(x+y)+10
a) \(P=3\left(x^2+2xy+y^2\right)-2\left(x+y\right)-100\)
\(P=3\left(x+y\right)^2-2.5-100\)
\(P=3.5^2-110\)
\(P=-35\)
b) \(Q=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3.5+10\)
\(Q=\left(x+y\right)^3-2\left(x+y\right)^2+25\)
\(Q=5^3-2.5^2+25\)
\(Q=100\)
Đúng 2
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
21 tháng 7 2023 lúc 15:38
Phân tích các đa thức sau thành nhân tử:
a) x3+y3+x+y
b) x3−y3+x−y
c) (x−y)3+(x+y)3
d) x3−3x2y+3xy2−y3+y2−x2
`a, x^3 + y^3 + x + y`
`= (x+y)(x^2-xy+y^2)+x+y`
`= (x+y)(x^2-xy+y^2+1)`
`b, x^3 - y^3 + x -y`
`= (x-y)(x^2+xy+y^2)+x-y`
`= (x-y)(x^2+xy+y^2+1)`
`c, (x-y)^3 + (x+y)^3`
`= (x-y+x+y)(x^2-2xy+y^2 - x^2 + y^2 + x^2 + 2xy + y^2)`
`= (2x)(x^2 + 3y^2)`
`d, x^3 - 3x^2y + 3xy^2 - y^3 + y^2 - x^2`
`= (x-y)^3 + (y-x)(x+y)`
`=(x-y)(x^2+2xy+y^2-x-y)`
Đúng 1
Bình luận (0)
a: =(x+y)(x^2-xy+y^2)+(x+y)
=(x+y)(x^2-xy+y^2+1)
b: =(x-y)(x^2+xy+y^2)+(x-y)
=(x-y)(x^2+xy+y^2+1)
c: =x^3-3x^2y+3xy^2-y^3+x^3+3x^2y+3xy^2-y^3
=2x^3+6xy^2
d: =(x-y)^3+(y-x)(y+x)
=(x-y)[(x-y)^2-(x+y)]
Đúng 0
Bình luận (0)
Phân tích thành nhân tử: x 3 - x + 3 x 2 y + 3 x y 2 + y 3 - y
x 3 - x + 3 x 2 y + 3 x y 2 + y 3 - y = x 3 + 3 x 2 y + 3 x y 2 + y 3 - x - y = x + y 3 - x - y = x + y x + y 2 - 1 = x + y x + y + 1 x + y - 1
Đúng 0
Bình luận (0)
x3– x + 3x2y + 3xy2 + y3– y=? (Phân tích đa thức thành nhân tử)
\(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left(x^2+2xy+y^2-1\right)\)
Đúng 1
Bình luận (0)
\(x^3-x+3x^2+3xy^2+y^3-y\)
\(=\left(x+y\right)^3-\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
Đúng 1
Bình luận (0)
= (x3 + 3x2y + 3xy2 + y3) - (x+y)
= (x + y)3 - (x + y)
= (x + y).[(x+y)2 - 1 ]
= (x + y).(x + y - 1).(x + y + 1)
Đúng 1
Bình luận (3)
Tính giá trị biểu thức:
a) M=x2-2xy+y2-10x+10y với x-y=9
b) N=x3+3x2y+3xy2+y3+x2+2xy+y2 với x=10-y
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
Đúng 1
Bình luận (0)
Giá trị biểu thức - x 3 + 3 x 2 y - 3 xy 2 + y 3 tại x = -2, y = 1 là
Giá trị của biểu thức
-
x
3
+
3
x
2
y
-
3
xy
2
+
y
3
tại x 5, y 7 là
Đọc tiếp
Giá trị của biểu thức - x 3 + 3 x 2 y - 3 xy 2 + y 3 tại x = 5, y = 7 là