Cho tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh ABCD là hình thang.

Những câu hỏi liên quan
1. Cho hình thang ABCD(AB//CD). M là trung điểm của BC. Cho biết DM là tia phân giác của góc D. Chứng minh rằng tia AM là tia phân giác của góc A.
2.Tứ giác ABCD có AD=BC và AC=BD. Chứng minh rằng ABCD là hình thang cân.
Xét ▲ADC và ▲BCD có:
AD = BC ( gt )
AC = BD ( gt )
DC chung
=> ▲ADC = ▲BCD ( c.c.c )
=> góc D = góc C ( c.t.ứ )
cmtt ta đc góc A = Góc B
Mà Góc D + góc A + Góc C + Góc B=360o
=> 2GócA+2GócD=360o
-> gócA+gócD=180o ( 2 góc trong cùng phía )=>AB//DC -> ABCD là hình thang
Vì góc D = góc C (cmt) nên ABCD là hình thang cân
tứ giác abcd có ab = bc và ac là tia phân giác của góc a chứng minh rằng abcd là hình thang
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
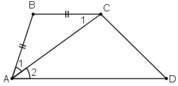
* Để chứng minh ABCD là hình thang ta cần chứng minh AD // BC.
Thông thường để chứng minh hai đường thẳng song song ta có thể chọn một trong các cách:
+ Chứng minh hai góc so le trong bằng nhau hoặc hai góc đồng vị bằng nhau.
+ Chứng minh hai đường thẳng cùng song song hoặc cùng vuông góc với đường thẳng thứ ba.
Ở bài này ta sẽ đi chứng minh hai góc so le trong bằng nhau là góc A2 và C1.
Theo giả thiết ta có:

Mà hai góc này ở vị trí so le trong
⇒ AD // BC
Vậy ABCD là hình thang (đpcm).
Đúng 2
Bình luận (0)
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
Cho tứ giác ABCD có AB = BC AC là tia phân giác của góc C Chứng minh tứ giác ABCD là hình thang
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{DAC}\)
nên \(\widehat{DAC}=\widehat{BCA}\)
mà hai góc ở vị trí so le trong
nên AD//BC
hay ABCD là hình thang
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB=BC và AC là tia phân giác của góc A. Chứng minh ABCD là hình thang.
Tự vẽ hình
Tâ có: AB=BC (gt)
=> t/g ABC cân tại A
=> góc BAC = góc BCA
Mà góc BAC = góc CAD (AC là tia p/g của góc A)
=>góc CAD = góc BCA
Mà góc CAD và góc BCA là 2 góc ở vị trí so le trong
=> AB // CD
=> ABCD là hình thang
Đúng 1
Bình luận (0)
Theo bài , ta có :
\(+AB=BC\Rightarrow\Delta ABC\)cân tại B
\(\Rightarrow\widehat{A_1}=\widehat{C_1}\left(1\right)\)
+ AC là tia phân giác góc A
\(\Rightarrow\widehat{A_2}=\widehat{A_1}\left(2\right)\)
Từ (1)(2) , suy ra : \(\widehat{A_2}=\widehat{C_1}\left(=\widehat{A_1}\right)\)
Mà hai góc này ở vị trí so le trong
=> AD // BC
Vậy ABCD là hình thang (đpcm)
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang ?
Bài giải:
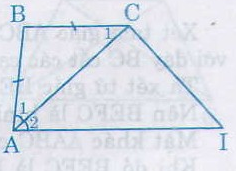
Ta có AB = BC (gt)
Suy ra ∆ABC cân
Nên (1)
Lại có (2) (vì AC là tia phân giác của )
Từ (1) và (2) suy ra
nên BC // AD (do ở vị trí so le trong)
Vậy ABCD là hình thang
Đúng 2
Bình luận (0)
Ta có AB = BC (gt)
Suy ra: ∆ABC cân.
Nên \(\widehat{A_1}=\widehat{C_1}\) (1)
Lại có \(\widehat{A_1}=\widehat{A_2}\) (2) (vì AC là tia phân giác của ˆAA^)
Từ (1) và (2) suy ra \(\widehat{C_1}=\widehat{A_2}\)
nên BC // AD (do \(\widehat{A_1};\widehat{C_2}\) ở vị trí so le trong)
Vậy ABCD là hình thang.
Đúng 0
Bình luận (0)
Tứ giác ABCD có AB= BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang. ( vẽ giúp mình luôn hình ạ )




















