Chứng minh x,y thuộc Q thì |x+y| ≤ |x| + |y|
Khi nao dấu đẳng thức xảy ra
chứng minh bất đẳng thức: 1/x +1/y +1/z >= 9/(x+y+z) dấu “=” xảy ra khi x = y = z,
+) Áp dụng BĐT Cô - si cho 4 số dương x; x; y; z ta có:
x+x+y+z≥44√x.x.y.z
=> 2x + y + z ≥44√x.x.y.z (1)
Với 4 số dương 1x ;1x ;1y ;1z ta có: 1x +1x +1y +1z ≥4.4√1x .1x .1y .1z (2)
Từ (1)(2) => (2x+y+z)(1x +1x +1y +1z )≥4.4√x.x.y.z4.4√1x .1x .1y .1z =16
=> 12x+y+z ≤116 .(2x +1y +1z ) (*)
Tương tự, ta có: 1x+2y+z ≤116 .(1x +2y +1z ) (**)
1x+y+2z ≤116 .(1x +1y +2z ) (***)
Từ (*)(**)(***) => Vế trái ≤116 (4x +4y +4z )=14 .(1x +1y +1z )=14 .4=1
=> đpcm
Áp dụng BĐT Cauchy- schwarz:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{\left(1+1+1\right)^2}{x+y+z}=\frac{9}{x+y+z}\)
(Dấu "="\(\Leftrightarrow x=y=z\))
Có x>0, y>0. Chứng minh: \(\dfrac{\sqrt{x}}{\sqrt{y}}+\dfrac{\sqrt{y}}{\sqrt{x}}\)>_2
Dấu đẳng thức xảy ra khi nào ?
\(\sqrt{\dfrac{x}{y}}-2.\sqrt{\sqrt{\dfrac{x}{y}}}.\sqrt{\sqrt{\dfrac{y}{x}}}+\sqrt{\dfrac{y}{x}}+2.\sqrt{\sqrt{\dfrac{x}{y}}.\sqrt{\dfrac{y}{x}}}\)
=\(\left(\sqrt{\sqrt{\dfrac{x}{y}}}-\sqrt{\sqrt{\dfrac{y}{x}}}\right)^2+2\)
lớn hơn hoặc bằng 2
dấu = xảy ra <=>
\(\left(\sqrt{\sqrt{\dfrac{x}{y}}}-\sqrt{\sqrt{\dfrac{y}{x}}}\right)^2+2=2\)
=>\(\sqrt{\sqrt{\dfrac{x}{y}}}=\sqrt{\sqrt{\dfrac{y}{x}}}\)
=>\(\dfrac{x}{y}=\dfrac{y}{x}\)
=>x2=y2
=>x=y
CMR:x thuộc số hữu tỉ |x + y| \(\le\) |x| + |y|
hỏi khi nào dấu đẳng thức xảy ra
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số a, b, c không âm thì x 3 + y 3 + z 3 3 ≥ x y z
(Bất đẳng thức Cô-si cho ba số không âm)
Dấu đẳng thức xảy ra khi ba số a, b, c bằng nhau.
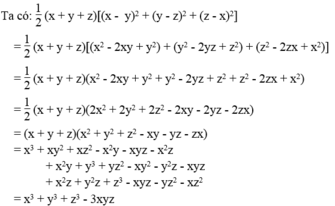
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
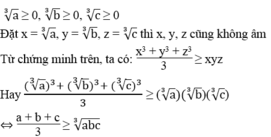
Lâu lâu đăng bài giải trí!
Chứng minh bất đẳng thức sau:
\(3\left(x^2-x+1\right)\left(y^2-y+1\right)\ge2\left(x^2y^2-xy+1\right);\forall x,y\inℝ\)
Dấu "=" xảy ra khi nào???
Giải xàm tí ạ!\(VT-VP=\frac{1}{2}\left[\left(x^2-3x+1\right)^2+\left(y^2-3y+1\right)^2+\left(x-y\right)^2\left(5-x-y\right)\left(x+y-1\right)\right]\ge0\)
=> qed
??? KHang ơi! Sai rồi ? Tại sao VT - Vp = 1/2. Dòng thứ 2 ???
Nguyễn Linh Chi còn khúc dưới nữa mà cô, tại nó dài quá nên olm ko hiển thị hết trng một dòng. Mà bài đó em cũng làm xàm:)
Cho x,y là 2 số thực bất kỳ khác 0. Chứng minh rằng:
\(\frac{4x^2y^2}{\left(x^2+y^2\right)^2}+\frac{x^2}{y^2}+\frac{y^2}{x^2}\)\(\ge3\)
Dấu đẳng thức xảy ra khi nào ?
\(\frac{4x^2y^2}{\left(x^2+y^2\right)^2}+\frac{x^2}{y^2}+\frac{y^2}{x^2}\ge3\)
\(\Leftrightarrow\)\(\frac{4x^2y^2}{\left(x^2+y^2\right)^2}+\frac{x^2}{y^2}+\frac{y^2}{x^2}-3\ge0\)
\(\Leftrightarrow\frac{4x^4y^4+x^4\left(x^2+y^2\right)^2+y^4\left(x^2+y^2\right)^2-3x^2y^2\left(x^2+y^2\right)^2}{x^2y^2\left(x^2+y^2\right)^2}\ge0\)
\(\Leftrightarrow4x^4y^4+x^4\left(x^4+2x^2y^2+y^4\right)+y^4\left(x^4++2x^2y^2+y^4\right)-3x^2y^2\left(x^4+2x^2y^2+y^4\right)\ge0\)
\(\Leftrightarrow4x^4y^4+x^8+2x^6y^2+x^4y^4+x^4y^4+2x^2y^6+y^8-3x^6y^2-6x^4y^4-3x^2y^6\ge0\)
\(\Leftrightarrow x^8+y^8-x^6y^2-x^2y^6\ge0\)
\(\Leftrightarrow x^6\left(x^2-y^2\right)-y^6\left(x^2-y^2\right)\ge0\)
\(\Leftrightarrow\left(x^2-y^2\right)^2\left(x^4+x^2y^2+y^4\right)\ge0\)( luôn đúng )
=> \(\frac{4x^2y^2}{\left(x^2+y^2\right)^2}+\frac{x^2}{y^2}+\frac{y^2}{x^2}\ge3\)
Dấu " = " xảy ra <=> x=y
Giải bài toán sau bằng phương pháp chứng minh phản chứng: “Chứng minh rằng với mọi x, y, z bất kì thì các bất đẳng thức sau không đồng thời xảy ra x < y − z ; y < z − x ; z < x − y ”
Một học sinh đã lập luận tuần tự như sau:
(I) Giả định các đẳng thức xảy ra đồng thời.
(II) Thế thì nâng lên bình phương hai vế các bất đẳng thức, chuyển vế phải sang vế trái, rồi phân tích, ta được:
(x – y + z)(x + y – z) < 0
(y – z + x)(y + z – x) < 0
(z – x + y)(z + x – y) < 0
(III) Sau đó, nhân vế theo vế ta thu được:(x – y + z ) 2 (x + y – z)(-x + y + z) < 0 (vô lí)
Lý luận trên, nếu sai thì sai từ giai đoan nào?
A. (I)
B. (II)
C. (III)
D. Lý luận đúng
1)Với hai số dương x và y, chứng minh rằng \(\frac{\left(x+y\right)^2}{2}+\frac{x+y}{4}\ge x\sqrt{y}+y\sqrt{x}\)
Đẳng thức xảy ra khi nào ?
Cách khác:
\(\frac{\left(x+y\right)^2}{2}+\frac{\left(x+y\right)}{4}\ge2xy+\frac{x+y}{4}\)
\(=\frac{4xy+x+4xy+y}{4}=\frac{x\left(4y+1\right)+y\left(4x+1\right)}{4}\)
\(\ge\frac{4x\sqrt{y}+4y\sqrt{x}}{4}=x\sqrt{y}+y\sqrt{x}\)
Dấu = xảy ra khi \(x=y=\frac{1}{4}\)
\(\frac{1}{2}\left(x+y\right)\left(x+y+\frac{1}{2}\right)=\frac{1}{2}\left(x+y\right)\left(x+\frac{1}{4}+y+\frac{1}{4}\right)\)
Áp dụng bất đẳng thức cauchy:
\(x+y\ge2\sqrt{xy}\)
\(x+\frac{1}{4}\ge2\sqrt{\frac{x}{4}}=\sqrt{x}\)
\(y+\frac{1}{4}\ge2\sqrt{\frac{y}{4}}=\sqrt{y}\)
do đó \(VT\ge\frac{1}{2}.2.\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)=x\sqrt{y}+y\sqrt{x}\)(đpcm)
Dấu = xảy ra khi \(x=y=\frac{1}{4}\)
Cho các số thực dương x,y thỏa mãn \(x+y>=3\). Chứng minh :\(x+y+\dfrac{1}{2x}+\dfrac{1}{2y}>=\dfrac{9}{2}\) Đẳng thức xảy ra khi nào?