cho hàm số y =\(\sqrt{x^2+\sqrt{x^2+4x+4}}\)
1. tìm tập xác định của hàm số
2. rút gọn y( loại bỏ dấu căn và dấu giá trị tuyệt đối)
3. vẽ đồ thị hàm số
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị hàm số tìm giá trị max của y, giá trị min của y
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Cho hàm số \(y=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
a) Vẽ đồ thị hàm số
b) Dùng đồ thị tìm giá trị max của y, giá trị min của y
1. Rút gọn
A=\(\sqrt{2}\left(\sqrt{8}-3\right)+\sqrt{18}\)
2.
a) Cho hàm số y=ax-3, biết đồ thị hàm số đi qua điểm A(-3:18). Tìm a và xác định công thức hàm số.
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình: y=(m+1)x-n. Viết phương trình của d, biết d đi qua điểm A(1:-1) và có hệ số góc bằng -3
Bài 2:
a: Thay a=-3 và y=18 vào (d), ta được:
-3a-3=18
=>-3a=21
=>a=-7
b: Vì d có hệ số góc bằng -3 nên m+1=-3
=>m=-4
Thay x=1 và y=-1 vào y=-3x-n, ta được:
-3*1-n=-1
=>n+4=1
=>n=-3
Cho hàm số y=m!x!+2 x.
a,Xác định m biết đồ thị hàm số đi qua A(1;1).
b, Vẽ đồ thị của hàm số
ps: Trình bày giúp mk nhé và chỗ !x! là giá trị tuyệt đối của x nha
Trong hệ trục toạ độ Oxy cho hàm số y = 3x + m (*).
1) Tìm giá trị của m để đồ thị của hàm
a) A(-1; 3); b) B(\(\sqrt{2};-5\sqrt{2}\)); c) C(2 ; -1).
2) Xác định m để đồ thị của hàm số (*) cắt đồ thị của hàm số y = 2x - 1 tại điểm nằm trong góc vuông phần tư thứ IV.
2) Phương trình hoành độ giao điểm là:
3x+m=2x-1
\(\Leftrightarrow3x-2x=-1-m\)
\(\Leftrightarrow x=-m-1\)
Để (*) cắt đồ thị của hàm số y=2x-1 tại điểm nằm trên góc vuông phần tư thứ IV thì \(\left\{{}\begin{matrix}x>0\\y< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-m-1>0\\2x-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-m>1\\2\left(-m-1\right)-1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-2m-2-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-2m< 3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\m>\dfrac{-3}{2}\end{matrix}\right.\Leftrightarrow-\dfrac{3}{2}< m< -1\)
Bài 2 : Cho hàm số f(x) xác định bởi công thức : y= f(x) = |x-1| - 2
Hãy viết hàm số về dạng không còn dấu giá trị tuyệt đối
Bài 3 : Cho hàm số : y = f(x) = | x+ 1 | + | x+ 5 | -6
Hãy viết công thức đã cho về dạng không còn dấu giá trị tuyệt đối . Từ đó tìm giá trị nhỏ nhất của hàm số
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
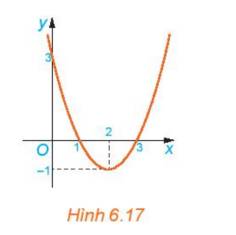
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
CÂU 1 : cho biểu thức P = ✔49x - ✔16x + ✔25x -1
a, tính giá trị của x = 4
b, rút gọn biểu thức P
CÂU 2: cho hàm số bậc nhất y = (m+1) . x+2 a, vẽ đồ thị hàm số khi x=0 b, xác định m để đồ thị hàm số để cắt trục hoành tại điểm có tung độ = 4
CÂU 3: cho đường tròn tâm O , gọi H là trung điểm của OA , đường thẳng vuông góc với OA tại H cắt đường tròn tâm O tại B và C . kẻ đường tròn tâm O tại B cắt đường thẳng OA tại M a, tính độ dài M b, chứng minh MC là tiếp tuyến của đường tròn tâm O
Câu 1:
a: Khi x=4 thì \(P=\sqrt{49\cdot4}-\sqrt{16\cdot4}+\sqrt{25\cdot4}-1=7\cdot2-8\cdot2+5\cdot2-1=7\)
b: \(P=7\sqrt{x}-4\sqrt{x}+5\sqrt{x}-1=8\sqrt{x}-1\)