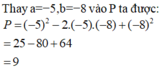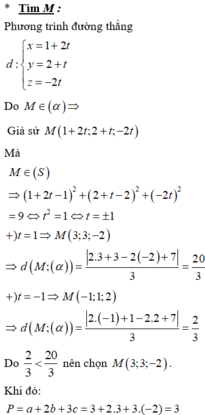Cho a = 5 + b. Tính giá trị của biểu thức M = a2+b2+2a-2b-2ab+65

Những câu hỏi liên quan
Tính giá trị biểu thức:a) M (a - 2b)(
a
2
+ 2ab + 4
b
2
) +
(
2
b
-
a
)
3
tại a -1; b 2;b) N (2xy - 2)(2xy + 3) -
(
1
-
...
Đọc tiếp
Tính giá trị biểu thức:
a) M = (a - 2b)( a 2 + 2ab + 4 b 2 ) + ( 2 b - a ) 3 tại a = -1; b = 2;
b) N = (2xy - 2)(2xy + 3) - ( 1 - 2 xy ) 2 tại x = 1 2 ; y = -1.
a) Rút gọn M = -6ab(-2b + a). Tính được M = 60.
b) Rút gọn M = 6xy – 7. Tính được N = -10.
Đúng 0
Bình luận (0)
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
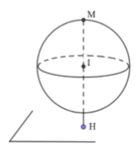
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất





Đúng 0
Bình luận (0)
Tính giá trị biểu thức P = a 2 - 2 a b + b 2 khi a = - 5;b = - 8.
A. 9
B. -9
C. -6
D. 6
Cho các số thực a, b, c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
-
4
b
4
. Tính P a + 2b + 3c khi biểu thức đạt giá trị lớn nhất A. 7. B. 3 C. -3. D. -7.
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a 2 + b 2 + c 2 - 2 a - 4 b = 4 . Tính P = a + 2b + 3c khi biểu thức đạt giá trị lớn nhất
A. 7.
B. 3
C. -3.
D. -7.
Tính giá trị của biểu thức: a 2 + 2 ab + b 2 − 1 với a = -2, b = 4
Thay a = -2, b = 4 vào biểu thức ta được:
( − 2 ) 2 + 2. ( − 2 ) .4 + 4 2 − 1 = 4 + ( − 16 ) + 16 − 1 = 3
Đúng 0
Bình luận (0)
`a^2 + 2ab+b^2-1`
`= (a+b)^2-1`
`=(a+b)^2 - 1^2`
`=(a+b-1)(a+b+1)`
`= (-2+4-1)(-2+4+1)`
`= 3`
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?A. (A – B)2 A2 – 2AB + B2 B. (A + B)2 A2 + 2AB + B2C. A2 – B2 (A + B)(A – B) D. A3 – B3 (A – B)(A2 + AB + B2)
Đọc tiếp
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Cho ba số a,b,c thỏa mãn đồng thời 3 điều kiện: a2 + 2b + 10; b2 + 2c + 10; c2 + 2a +1 0. Tính giá trị biểu thức: A a2003 + b2009 + c2011.
Đọc tiếp
Cho ba số a,b,c thỏa mãn đồng thời 3 điều kiện: a2 + 2b + 1=0; b2 + 2c + 1=0; c2 + 2a +1 =0. Tính giá trị biểu thức: A= a2003 + b2009 + c2011.
Tính giá trị biểu thức:a) M (7 – m)(
m
2
+ 7m + 49) – (64 –
m
3
) tại m 2017;b*) N 8
a
3
– 27
b
3
biết ab 12 và 2a – 3b 5;c) K
a
3
+
b
3
+ 6
a
2
b
2...
Đọc tiếp
Tính giá trị biểu thức:
a) M = (7 – m)( m 2 + 7m + 49) – (64 – m 3 ) tại m = 2017;
b*) N = 8 a 3 – 27 b 3 biết ab = 12 và 2a – 3b = 5;
c) K = a 3 + b 3 + 6 a 2 b 2 (a + b) + 3ab( a 2 + b 2 ) biết a + b = 1.
a) Rút gọn M = 279. Với m = 2017 giá trị của M = 279.
b) N = 8 a 3 - 27 b 3 = ( 2 a ) 3 - ( 3 b ) 3 = ( 2 a - 3 b ) 3 + 3.2a.3b.(2a - 3b)
Thay a.b = 12;2a - 3b = 5 ta thu được N - 1205.
c) Cách 1: Từ a + b = 1 Þ a = 1 - b thế vào K.
Thực hiện rút gọn K, ta có kết quả K = 1.
Cách 2: Tìm cách đưa biêu thức về dạng a + b.
a 3 + b 3 = ( a + b ) 3 – 3ab(a + b) = 1 - 3ab;
6 a 2 b 2 (a + b) = 6 a 2 b 2 kết hợp với 3ab( a 2 + b 2 ) bằng cách đặt 3ab làm nhân tử chung ta được 3ab( a 2 + 2ab + b 2 ) = 3ab.
Thực hiện rút gọn K = 1.
Đúng 0
Bình luận (0)
Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: A = a(a2 + 2b) + b(b2– a).
\(a+b=1\)
\(\Rightarrow a^2+2ab+b^2=1\)
\(\Rightarrow\left(a^2+b^2\right)+2ab=1\)
\(\Rightarrow2ab+2ab\le1\) (do \(a^2+b^2\ge2ab\))
\(\Rightarrow ab\le\dfrac{1}{4}\)
\(A=a\left(a^2+2b\right)+b\left(b^2-a\right)\)
\(=a^3+2ab+b^3-ab\)
\(=a^3+b^3+ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+ab\)
\(=1^3-3ab+ab=1-2ab\ge1-2.\dfrac{1}{4}=\dfrac{1}{2}\)
\(A_{min}=\dfrac{1}{2}\Leftrightarrow a=b=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
\(a+b=1\Rightarrow a=\dfrac{1}{2}+x;b=\dfrac{1}{2}+y\left(x+y=0\right)\)
có: \(A=a\left(a^2+2b\right)+b\left(b^2-a\right)=a^3+b^3+ab=a^2+b^2\\ =\left(\dfrac{1}{2}+x\right)^2+\left(\dfrac{1}{2}+y\right)^2=\dfrac{1}{2}+x^2+y^2\ge\dfrac{1}{2}\)
\(\Rightarrow A_{min}=\dfrac{1}{2}\Leftrightarrow x=y=0\Leftrightarrow a=b=\dfrac{1}{2}\)
Đúng 1
Bình luận (2)