Chứng minh đa thức sau vô nghiệm
X4+2x3+3x2+2x+1
Những câu hỏi liên quan
Bài 1: Rút gọn biểu thức sau:a. 3x2(2x3- x+5) - 6x5-3x3+10x2b. -2x(x3-3x2-xx+11)-2x4+3x3+2x2-22x2xBài 2: Chứng minh biểu thức sau không phụ thuộc vào x:a. x(2x+1)-x2(x+2)+(x2-x+3)b. 4(x-6)-x2(2+3x)+x(5x-4)+3x2(x-1)Bài 3: Cho đa thức: f(x)3x2-x+1 g(x)x-1a. Tính f(x).g(x)b. Tìm x để f(x).g(x)+x2[1-3g(x)]Bài 4: Tìm x:a. dfrac{1}{4}x2-(dfrac{1}{2}x-4)dfrac{1}{2}x-14b. 2x(x-4)+3(x-4)+x(x-2)-5(x-2)3x(x-4)-5(x-4)Các bạn giúp mik giải bt nha. Cảm ơn mn nhiêu ạ.
Đọc tiếp
Bài 1: Rút gọn biểu thức sau:
a. 3x2(2x3- x+5) - 6x5-3x3+10x2
b. -2x(x3-3x2-xx+11)-2x4+3x3+2x2-22x2x
Bài 2: Chứng minh biểu thức sau không phụ thuộc vào x:
a. x(2x+1)-x2(x+2)+(x2-x+3)
b. 4(x-6)-x2(2+3x)+x(5x-4)+3x2(x-1)
Bài 3: Cho đa thức: f(x)=3x2-x+1
g(x)=x-1
a. Tính f(x).g(x)
b. Tìm x để f(x).g(x)+x2[1-3g(x)]=
Bài 4: Tìm x:
a. \(\dfrac{1}{4}\)x2-(\(\dfrac{1}{2}\)x-4)\(\dfrac{1}{2}\)x=-14
b. 2x(x-4)+3(x-4)+x(x-2)-5(x-2)=3x
(x-4)-5(x-4)
Các bạn giúp mik giải bt nha. Cảm ơn mn nhiêu ạ.
`@` `\text {Ans}`
`\downarrow`
Gửi c!
Đúng 5
Bình luận (1)
Bài 1:
a) \(3x^2\left(2x^3-x+5\right)-6x^5-3x^3+10x^2\)
\(=6x^5-3x^3+10x^2-6x^5-3x^3+10x^2\)
\(=10x^2+10x^2\)
\(=20x^2\)
b) \(-2x\left(x^3-3x^2-x+11\right)-2x^4+3x^3+2x^2-22x\)
\(=-2x^4+6x^3+2x^2-22x-2x^4+3x^3+2x^2-22x\)
\(=-4x^4+9x^3+4x^2-44x\)
Đúng 0
Bình luận (2)
4:
a: =>1/4x^2-1/4x^2+2x=-14
=>2x=-14
=>x=-7
b: =>2x^2-8x+3x-12+x^2-2x-5x+10=3x^2-12x-5x+20
=>3x^2-12x-2=3x^2-17x+20
=>5x=22
=>x=22/5
Đúng 1
Bình luận (0)
Chọn đa thức mà em cho là kết quả đúng:
(2x3 – 2x + 1) – (3x2 + 4x – 1) ?
2x3 + 3x2 – 6x + 2
2x3 – 3x2 – 6x + 2
2x3 – 3x2 + 6x + 2
2x3 – 3x2 – 6x – 2
Đọc tiếp
Chọn đa thức mà em cho là kết quả đúng:
| (2x3 – 2x + 1) – (3x2 + 4x – 1) = ? | 2x3 + 3x2 – 6x + 2 |
| 2x3 – 3x2 – 6x + 2 | |
| 2x3 – 3x2 + 6x + 2 | |
| 2x3 – 3x2 – 6x – 2 |
Đặt và thực hiện phép tính ta có :
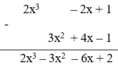
Vậy chọn đa thức thứ hai.
Đúng 0
Bình luận (0)
giúp mik với.
câu 4.Tính tổng của hai đa thức A (x)= 2x3 + 3x2 - 2x + 1 và B(x) = 2x3 + 5x - 4.
`A(x)+B(x)=`\((2x^3+3x^2-2x+1)+(2x^3+5x-4)\)
`=2x^3+3x^2-2x+1+2x^3+5x-4`
`= (2x^3+2x^3)+3x^2+(-2x+5x)+(1-4)`
`= 4x^3+3x^2+3x-3`
Đúng 1
Bình luận (1)
Phân tích các đa thức sau thành nhân tử
a,x4+2x3+3x2+2x+1
b,x4-4x3+2x2+4x+1
c,x4+x3+2x2+2x+4
7 tháng 2 2022 lúc 13:23
Tìm tất cả các đa thức thỏa: x4 + 2x3 +3x2 + 2x + 1 = P2(x)
Help me!!!
Đặt d : deg P(x) , ta có:
\(4=d^2\Leftrightarrow d=2\)
\(\Rightarrow P\left(x\right)=ax^2+bx+c\left(a\ne0\right)\)
Trog đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
\(x^4+2x^3+6x^2-8x+8=x^4+bx^3+\left(4+c\right).x^2+4bx+4c\)
Tiến hành đồng nhất, ta được:
\(\left\{{}\begin{matrix}b=-2\\c=2\end{matrix}\right.\)
suy ra: \(P\left(x\right)=x^2-2x+2\)
Đúng 2
Bình luận (1)
Đặt d : deg P(x) , ta có:
4=d2⇔d=24=d2⇔d=2
⇒P(x)=ax2+bx+c(a≠0)⇒P(x)=ax2+bx+c(a≠0)
Trong đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
x^4+2x^3+6x^2−8x+8=x^4+bx^3(4+c).x^2+4bx+4c
Tiến hành đồng nhất, ta được:
suy ra: P(x)=x^2−2x+2
mình chỉ bít zậy ko biết có đúng không nữa 
Đúng 1
Bình luận (1)
Phân tích đa thức 2x3 + 3x2 - 2x thành nhân tử
\(=x\left(2x^2+3x-2\right)=x\left(2x^2+4x-x-2\right)=x\left[2x\left(x+2\right)-\left(x+2\right)\right]=x\left(2x-1\right)\left(x+2\right)\)
Đúng 2
Bình luận (0)
2x3 + 3x2 - 2x
= x ( 2x2 + 3x - 2 )
= x ( 2\(x^2\) + 4\(x-x-2\) )
= x [ ( 2\(x^2\) + 4x ) - ( x + 2 )]
= x [ 2x ( x + 2 ) - ( x + 2 )]
= x ( 2x - 1 ) ( x + 2 )
Đúng 0
Bình luận (0)
chứng minh giá trị các biểu thức sau không phụ thuộc vào biến x
a) x(2x + 1) - x2(x + 2) + (x3 - x + 3);
b) x(3x2 - x + 5) - (2x3 +3x - 16) - x(x2 - x + 2);
a) x(2x+1)-x2(x+2)+(x3-x+3)= 2x2+x-x3-2x2+x3-x+3= 3
b)x (3x2-x+5)-(2x3+3x-16)-x(x2-x+2)= 3x3-x2+5x-2x3-3x+16-x3+x2-2x= 16
Đúng 2
Bình luận (0)
Chứng minh giá trị của biểu thức sau không phụ thuộc vào x:
a) A= x(2x+1)-x2(x+2)+(x3-x+5)
b) B= x(3x2-x+5)-(2x3+3x-16)-x(x2-x+2)
a) \(A=x\left(2x+1\right)-x^2\left(x+2\right)+\left(x^3-x+5\right)\)
\(A=2x^2+x-x^3-2x^2+x^3-x+5\)
\(A=5\)
=> giá trị biểu thức ko phụ thuộc vào biến x
b) \(A=x\left(3x^2-x+5\right)-\left(2x^3+3x-16\right)-x\left(x^2-x+2\right)\)
=> \(A=3x^3-x^2+5x-2x^3-3x+16-x^3+x^2-2x\)
=> \(A=\)16
vậy giá trị của biểu thức A ko phụ thuộc vào biến x
Đúng 2
Bình luận (0)
16 tháng 9 2021 lúc 19:00
BÀI 1: NHÂN ĐƠN THỨC VỚI ĐA THỨC
1) 2x(3x2 - 5x +3)
2) \(-\dfrac{1}{2}x^2\) ( 2x3 - 4x +3)
3) -2x ( x2 + 5x -3)
4) x ( 3x2 - 2x +5)
5) 3xy2 ( 2x - 4y + 3xy)
1. 2x(3x2 - 5x + 3) = 6x3 - 10x2 + 6x
2. \(-\dfrac{1}{2}x^2\left(2x^3-4x+3\right)=-x^5+2x^3+\dfrac{-3}{2}x^2\)
3. -2x(x2 + 5x - 3) = -2x3 - 10x2 + 6x
4. x(3x2 - 2x + 5) = 3x3 - 2x2 + 5x
5. 3xy2(2x - 4y + 3xy) = 6x2y2 - 12xy3 = 9x2y3
Đúng 1
Bình luận (0)
Có bao nhiêu số nguyên x để giá trị của đa thức A
2
x
3
–
3
x
2
+ 2x + 2 chia hết cho giá trị của đa thức B
x
2
+ 1 A. 3 B. 4 C. 2 D. 1
Đọc tiếp
Có bao nhiêu số nguyên x để giá trị của đa thức A = 2 x 3 – 3 x 2 + 2x + 2 chia hết cho giá trị của đa thức B = x 2 + 1
A. 3
B. 4
C. 2
D. 1
Ta có A : B
Để giá trị của đa thức A = 2 x 3 – 3 x 2 + 2x + 2 chia hết cho giá trị của đa thức B = x 2 + 1 thì
5 ⁝ ( x 2 + 1)
Hay ( x 2 + 1) Є U(5) = {-1; 1; -5; 5}
+) x 2 + 1 = -1 ó x 2 = -2 (VL)
+) x 2 + 1 = 1 ó x 2 = 0ó x = 0 (tm)
+) x 2 + 1 = -5 ó x 2 = -6 (VL)
+) x 2 + 1 = 5 ó x 2 = 4 ó x = ± 2 ™
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)