tại sao 1-1=0

Những câu hỏi liên quan
tại sao khi 1+1 = 2 nhưng sao 1-1 =0 sao không phải bằng 2 mà lại bằng 0
vì nó là phép trừ chứ không phải phép cộng
Đúng 1
Bình luận (0)
Chỉ mình chỗ khoanh tròn màu đỏ: + Tại sao ra 2 trường hợp 0x1 ; x1 + dfrac{1}{sqrt{x}-1}le-1 ( làm sao ra được như này) + sqrt{x}-10 có phải từ x1 rồi lấy căn 2 vế rồi chuyển vế đúng không + Và tại sao gọi là hàm số và tại sao lại không tìm được GTLN + Còn GTNN thì sẽ như thế nào
Đọc tiếp
Chỉ mình chỗ khoanh tròn màu đỏ:
+ Tại sao ra 2 trường hợp 0<x<1 ; x>1
+ \(\dfrac{1}{\sqrt{x}-1}\le-1\) ( làm sao ra được như này)
+ \(\sqrt{x}-1>0\) có phải từ x>1 rồi lấy căn 2 vế rồi chuyển vế đúng không
+ Và tại sao gọi là hàm số và tại sao lại không tìm được GTLN
+ Còn GTNN thì sẽ như thế nào
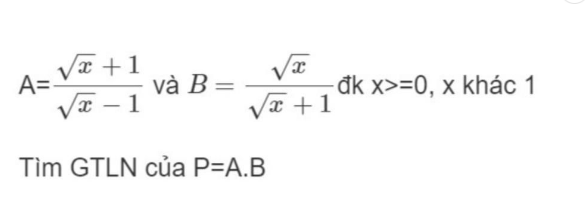

Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
Đúng 0
Bình luận (0)
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.
Đúng 0
Bình luận (3)
Cho A là 1 đa thức khác 0 tùy ý.Hãy giải thích tại sao 0/A=0 và A/A=1
ta có:
\(\dfrac{0}{A}=0\Leftrightarrow\dfrac{0}{A}=\dfrac{0}{1}\\ \Rightarrow0\cdot1=0\cdot A=0\\ \Rightarrow\dfrac{0}{A}=0\)
Đúng 0
Bình luận (0)
2n+1/n+2 > 0, ∀n ∈N* tại sao lại > 0
Lời giải:
Với mọi $n\in\mathbb{N}^*$ thì:
$2n+1>0$
$n+2>0$
Do đó thương của chúng là $\frac{2n+1}{n+2}>0$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
tại sao
2+8+9=10
0=1
1+9+8=1
1...1...1=6
tại sao con gà đi qua đường
Kb mik nhé
Bởi vì bạn bị thần kinh não giật hoặc bị rồ điên khùng khùng
Thế nhé
Đúng 0
Bình luận (0)
2 + 8 + 9 = 10
=> two + eight + nine = ten = 10
0 = 1
=> zero = one <=> o = o
1 + 9 + 8 = 1
=> one + eight + nine = one = 1
Tại sao 0 lại = 1?????
O giai thừa hay là gì:
Chào bạn, đúng là 0!=1 là do người ta quy ước, nhưng tại sao người ta quy ước như vậy mới là điều cần giải thích.
Thật ra trong toán học có nhiều phép toán phải quy ước vì thực tế không có mà người ta chỉ dựa vào tính chất cần có của nó mà gán cho.
Ví dụ 1: phép toán giữa hai số phức là quy ước, phép cộng còn có vẻ tự nhiên nhưng phép nhân hết sức bất thường.
Ví dụ 2: phép tính trong R mở rộng (có +vô cùng và -vô cùng) cũng là sự quy ước, chẳng hạn 2. (+vô cùng)=(+vô cùng).
Còn một số phép tính đặc biệt như 0!, 2^0, 5^0 đều được quy ước bằng 1, lí do là dựa vào tính chất. Các phép tính trên đều có thể quy về dạng "không có số nào nhân với nhau".
Nếu bạn chú ý 1 tính chất của phép nhân n số:
"Tích của n số là 1 số mà khi lấy bất kì số A nào nhân với tích đó thì được kết quả bằng lấy A nhân lần lượt liên tiếp n số trên"
Vậy tích của phép nhân 0 số theo tính chất này sẽ là một số mà khi lấy bất kì số A nào nhân với tích đó thì bằng A không nhân thêm gì nữa, nghĩa là A. (kết quả)=A. Vậy kết quả cần quy ước bằng 1.
Vậy là người ta đã dựa vào tính chất trên để quy ước 0!=a^0=1.
Đúng 0
Bình luận (0)
Tại sao 1 – √5 lại nhỏ hơn 0?
Ta có:
\(\sqrt{5}>\sqrt{4}=2\)
⇒ \(\left(1-\sqrt{5}\right)< \left(1-\sqrt{4}\right)=-1\)
⇒ \(\left(1-\sqrt{5}\right)< 0\)
Đúng 2
Bình luận (0)
vì \(\sqrt{5}=2.236\)
nếu 1-2,236=-1,236
do -1,236 là số âm mà số âm luôn nhỏ hơn 0
nên 1-\(\sqrt{5}\)<0
Đúng 0
Bình luận (0)
1=1=2=3=4=5=7=8=1=0.Tại sao lại như thế?
5+1=7 vì 5+1=6 xóa số 5 đi nên bằng 6+1=7;còn 7-1=3 vì 3+1=4 xóa số 1 đi nên bằng 7-4=3
Tại sao N0=1





























