Biểu thức  x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x  ≠  5.

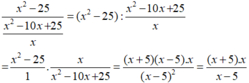
Ta có: 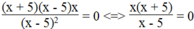khi x(x + 5) = 0 và x – 5  ≠  0

x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5

x = 0 không thỏa mãn điều kiện.

Vậy x = - 5 thì biểu thức  x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.

Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5  xác định khi x ≠ 5 và x  ≠  - 5

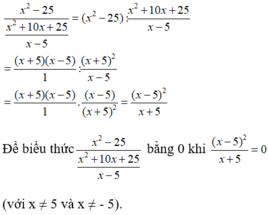
x - 5 2  = 0 ⇔ x – 5 = 0 ⇔ x= 5

x = 5 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để biểu thức  x 2 - 25 x 2 + 10 x + 25 x - 5 có giá trị bằng 0.

\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)

b:

\(D=-25x^2+10x-1-10\)

\(=-\left(25x^2-10x+1\right)-10\)

\(=-\left(5x-1\right)^2-10< =-10\)

Dấu = xảy ra khi x=1/5

\(E=-9x^2-6x-1+20\)

\(=-\left(9x^2+6x+1\right)+20\)

\(=-\left(3x+1\right)^2+20< =20\)

Dấu = xảy ra khi x=-1/3

\(F=-x^2+2x-1+1\)

\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)

Dấu = xảy ra khi x=1

\(25x^2-9=0\\ \Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x=3\\5x=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\x=\dfrac{3}{5}\end{matrix}\right.\)

=>(5x-3)(5x+3)=0

=>5x-3=0 hoặc 5x+3=0

=>x=3/5 hoặc x=-3/5

Hướng dẫn giải:

Điều kiện xác định của phân thức: x   ≠   0 ,   x   ≠   5

Ta có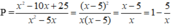 

Để P nhận giá trị nguyên thì 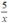 nguyên. Hay x là ước của 5. Ta có Ư(5) = { 1;-1;5;-5}.

Vì điều kiện xác định của phân thức là x ≠ 0, x≠ 5

Vậy x ∈ { 1;-1;-5} thì giá trị phân thức 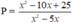 là nguyên

Ta có: 

\(P=\dfrac{5x-4y}{5x+4y}\)

\(\Leftrightarrow P^2=\left(\dfrac{5x-4y}{5x+4y}\right)^2\)

\(\Leftrightarrow P^2=\dfrac{\left(5x-4y\right)^2}{\left(5x+4y\right)^2}\)

\(\Leftrightarrow P^2=\dfrac{\left(5x\right)^2-2\cdot5x\cdot4y+\left(4y\right)^2}{\left(5x\right)^2+2\cdot5x\cdot4y+\left(4y\right)^2}\)

\(\Leftrightarrow P^2=\dfrac{\left(25x^2+16y^2\right)-40xy}{\left(25x^2+16y^2\right)+40xy}\)

Thay \(25x^2+16y^2=50xy\) vào ta có:

\(P^2=\dfrac{50xy-40xy}{50xy+40xy}=\dfrac{10xy}{90xy}=\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\)

Mà: \(4y< 5x< 0\)

Nên: \(P=\dfrac{5x-4y}{5x+4y}< 0\)

Vậy: \(P=-\dfrac{1}{3}\)

25x^2+16y^2=50xy

=>25x^2-50xy+16y^2=0

=>25x^2-10xy-40xy+16y^2=0

=>5x(5x-2y)-8y(5x-2y)=0

=>(5x-2y)(5x-8y)=0

=>5x=2y hoặc 5x=8y

5x>4y

=>5x=8y

=>x/8=y/5=k

=>x=8k; y=5k

\(P=\dfrac{5\cdot8k-4\cdot5k}{5\cdot8k+4\cdot5k}=\dfrac{40-20}{40+20}=\dfrac{1}{3}\)

x2&#x2212;10x+25x2&#x2212;5x=(x&#x2212;5)2x(x&#x2212;5)=x&#x2212;5x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x2−10x+25x2−5x=(x−5)2x(x−5)=x−5x

x&#x2212;5x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x−5x phải có giá trị nguyên.

x+12x&#x2212;2+3x2&#x2212;1&#x2212;x+32x+2)&#x22C5;(4x2&#x2212;45)" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)

x+12(x&#x2212;1)+3(x&#x2212;1)(x+1)&#x2212;x+32(x+1))&#x22C5;2(2x2&#x2212;2)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5

(x+1)2+6&#x2212;(x&#x2212;1)(x+3)2(x&#x2212;1)(x+1)&#x22C5;2&#x22C5;2(x2&#x2212;1)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5

(x+1)2+6&#x2212;(x2+3x&#x2212;x&#x2212;3)(x&#x2212;1)(x+1)&#x22C5;2(x&#x2212;1)(x+1)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5

25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25

25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25

25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25

2(x+1)25+185&#x2212;25x2&#x2212;45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline-table; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2(x+1)25+185−25x2−45x

2(x2+2x+1)5+185&#x2212;25x2&#x2212;45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2(x2+2x+1)5+185−25x2−45x

2x2+4x+25+185&#x2212;25x2&#x2212;45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+25+185−25x2−45x

2x2+4x+2+185&#x2212;25x2&#x2212;45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+2+185−25x2−45x

2x2+4x+205&#x2212;25x2&#x2212;45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+205−25x2−45x

c) tự làm, đkxđ: x≠1;x≠−1

ê k bn với mk ik

😘 😘 😘 😘

Biểu thức  x 2 - 25 x 2 - 10 x + 25 x xác định khi x 2 - 10 x + 25 ≠ 0 và x  ≠  0

x 2 - 10 x + 25   ≠  0 ⇔ x - 5 2   ≠  0 ⇔ x  ≠  5

Vậy điều kiện để biểu thức xác định là x  ≠  0 và x  ≠  5

Biểu thức  x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x 2 + 10 x + 25 ≠ 0 và x - 5  ≠  0

x 2 + 10 x + 25   ≠  0 ⇔ x + 5 2   ≠  0 ⇔ x  ≠  - 5

x – 5  ≠  0 ⇔ x  ≠  5

Vậy điều kiện để biểu thức xác định là x  ≠  5 và x  ≠  - 5.

vì trị tuyệt đối của 1 số luôn lớn hơn hoặc bằng 0 nên để

\(\left|x-y\right|+\left|y+\frac{9}{25}\right|=0\)

thì x-y=0 và y+9/25 =0

* y+9/25 = 0

=> y=-9/25

thay vào x-y=0 ta được

x-(-9/25)=0

=> x=-9/25