\(C=\dfrac{9+2\sqrt{x}}{2+3\sqrt{x}}\Rightarrow2C+3C\sqrt{x}=9+2\sqrt{x}\)

\(\Rightarrow\sqrt{x}\left(3C-2\right)=9-2C\)

\(\Rightarrow\sqrt{x}=\dfrac{9-2C}{3C-2}\ge0\Rightarrow\dfrac{2}{3}< C\le\dfrac{9}{2}\)

Mà C nguyên \(\Rightarrow C=\left\{1;2;3;4\right\}\)

- Với \(C=1\Rightarrow\sqrt{x}=\dfrac{9-2C}{3C-2}=7\Rightarrow x=49\)

- Với \(C=2\Rightarrow\sqrt{x}=\dfrac{9-2.2}{3.2-2}=\dfrac{5}{4}\Rightarrow x=\dfrac{25}{16}\)

... tương tự

C=9+2√x2+3√x⇒2C+3C√x=9+2√x

⇒√x(3C−2)=9−2C

⇒√x=9−2C3C−2≥0⇒23<C≤92 

Mà C nguyên ⇒C={1;2;3;4}

- Với C=1⇒√x=9−2C3C−2=7⇒x=49

- Với C=2⇒√x=9−2.23.2−2=54⇒x=2516

Bài 8:

\(M=1+\frac{4}{\sqrt{x}+1}\)

Để $M$ nguyên thì $\frac{4}{\sqrt{x}+1}$ nguyên 

Đặt $\frac{4}{\sqrt{x}+1}=t$ với $t$ là số nguyên dương 

$\Rightarrow \sqrt{x}+1=\frac{4}{t}$

$\sqrt{x}=\frac{4}{t}-1=\frac{4-t}{t}\geq 0$

$\Rightarrow 4-t\geq 0\Rightarrow t\leq 4$

Mà $t$ nguyên dương suy ra $t=1;2;3;4$

Kéo theo $x=9; 1; \frac{1}{9}; 0$

Kết hợp đkxđ nên $x=0; \frac{1}{9};9$

Bài 9:

$P=1+\frac{5}{\sqrt{x}+2}$

Để $P$ nguyên thì $\frac{5}{\sqrt{x}+2}$ nguyên 

Đặt $\frac{5}{\sqrt{x}+2}=t$ với $t\in\mathbb{Z}^+$

$\Leftrightarrow \sqrt{x}+2=\frac{5}{t}$

$\Leftrightarrow \sqrt{x}=\frac{5-2t}{t}\geq 0$

Với $t>0\Rightarrow 5-2t\geq 0$

$\Leftrightarrow t\leq \frac{5}{2}$

Vì $t$ nguyên dương suy ra $t=1;2$

$\Rightarrow x=9; \frac{1}{4}$ (thỏa đkxđ)

Bài 8: 

Để M nguyên thì \(\sqrt{x}+5⋮\sqrt{x}+1\)

\(\Leftrightarrow\sqrt{x}+1\inƯ\left(4\right)\)

\(\Leftrightarrow\sqrt{x}+1\in\left\{1;2;4\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)

hay \(x\in\left\{0;1;9\right\}\)

a: Khi x=9 thì \(A=\dfrac{17}{3+2}=\dfrac{17}{5}\)

b: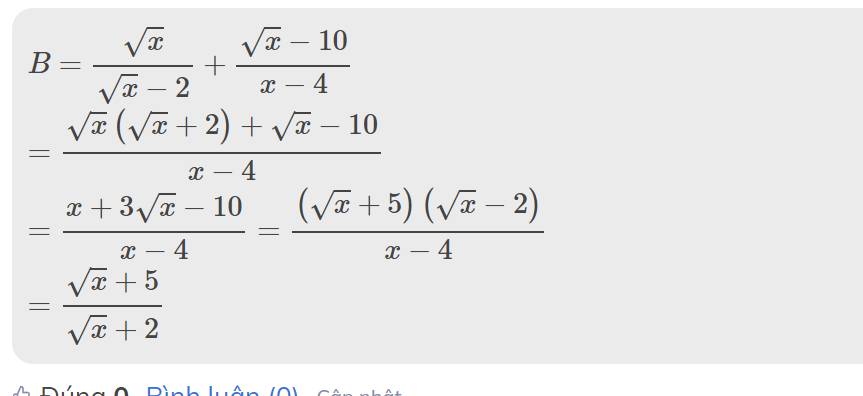 

c: P=A:B

\(=\dfrac{17}{\sqrt{x}+2}:\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{17}{\sqrt{x}+5}\)

Để P là số nguyên thì \(17⋮\sqrt{x}+5\)

mà \(\sqrt{x}+5>=5\) với mọi x thỏa mãn ĐKXĐ

nên \(\sqrt{x}+5=17\)

=>x=144

Lời giải:

ĐK: $x\geq 0; x\neq 4; x\neq 9$

a) 

\(P=\frac{2\sqrt{x}-9}{(\sqrt{x}-3)(\sqrt{x}-2)}+\frac{(2\sqrt{x}+1)(\sqrt{x}-2)}{(\sqrt{x}-3)(\sqrt{x}-2)}-\frac{(\sqrt{x}+3)(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}-2)}\)

\(=\frac{2\sqrt{x}-9+(2\sqrt{x}+1)(\sqrt{x}-2)-(\sqrt{x}+3)(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}-2)}=\frac{x-\sqrt{x}-2}{(\sqrt{x}-3)(\sqrt{x}-2)}\)

\(=\frac{(\sqrt{x}-2)(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-3}\)

b) \(P=\frac{\sqrt{x}+1}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)

Với $x$ nguyên, để $P$ nguyên thì $\sqrt{x}-3$ phải là ước nguyên của $4$

Mà $\sqrt{x}-3\geq -3$ nên:

$\Rightarrow \sqrt{x}-3\in\left\{\pm 1;\pm 2;4\right\}$

$\Rightarrow x\in \left\{4;16;1;25;49\right\}$ (đều thỏa mãn.

a) ĐKXĐ : \(\hept{\begin{cases}x\ge0\\x\ne1\\x\ne9\end{cases}}\)

b) \(P=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3x-3}{x-9}\right):\left(\frac{2\sqrt{x}-2}{\sqrt{x}+3}\right)\)

\(=\frac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\frac{\sqrt{x}+3}{2\left(\sqrt{x}-1\right)}=\frac{-3\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}=-\frac{3}{2\left(\sqrt{x}-3\right)}\)c) Để P nguyên thì \(2\left(\sqrt{x}-3\right)\in\left\{-3;-1;1;3\right\}\)=> x thuộc rỗng.