cho hình bình hành ABCD (AC>BD). Vẽ CE vuông góc với AB, CF vuông góc ới AD. CMR AB.AE+AD.AF=AC2

Những câu hỏi liên quan
Cho hình bình hành ABCD. Từ C kẻ CE vuông góc với AB, kẻ CF vuông góc với AD. Giả sử AC > BD. Chứng minh rằng: AB.AE + AD.AF = AC2.
Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với AB và CF vuông góc với AD. Chứng minh AB.AE + AD.AF = AC^2
Bài 2 : Cho hình bình hành ABCD, có đường chéo lớn AC. Từ C kẻ CE vuông góc AB, CF vuông góc AD ; BH vuông góc AC. Chứng minh : a) AB.AE = AH.AC b) BC.AF = AC.HC c) AB.AE + AD.AF = AC2 . d) Cho biết CE = 16cm, CF = 20cm, chu vi ABCD = 108cm. Tính diện tích ABCD
Giúp mk vs khó quá
Dựng BG ⊥ AC.
Xét ∆ BGA và ∆ CEA, ta có:
ˆBGA=ˆCEA=90∘BGA^=CEA^=90∘
ˆAA^ chung
Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)
Suy ra: ABAC=AGAEABAC=AGAE
Suy ra: AB.AE = AC.AG (1)
Xét ∆ BGC và ∆ CFA, ta có:
ˆBGC=ˆCFA=90∘;BGC^=CFA^=90∘
ˆBCG=ˆCAF;BCG^=CAF^ (so le trong vì AD // BC)
Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)
Suy ra: AFCG=ACBC⇒BC.AF=AC.CGAFCG=ACBC⇒BC.AF=AC.CG
Mà BC = AD (tính chất hình bình hành )
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế của đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
⇒AB.AE+AD.AF=AC(AG+CG)⇒AB.AE+AD.AF=AC(AG+CG)
Mà AG+CG=ACAG+CG=AC nên AB.AE+AD.AF=AC2
Đúng 2
Bình luận (0)
cho hình bình hành ABCD có AC > BD . Vẽ CE vuông góc với AB tại E và CF vuông góc với AD tại F . Biết đường chéo AC = a , hãy tính AB.AE + AD.AF theo a .
Cho hình bình hành ABCD (BC>CD). Vẽ CE vuông góc AB; FC vuông góc AD; BH vuông góc AC. Chứng minh rằng:
a) AB.AE=AH.AC
b) AB.AE+AD.AF=AC2
Giúp mình với mọi người ơi mình đang cần gấp THANKS TRƯỚC NHA!
a: Xet ΔAHB vuông tại H và ΔAEC vuông tại E có
góc EAC chung
=>ΔAHB đồng dạng với ΔAEC
=>AH/AE=AB/AC
=>AH*AC=AE*AB
b: Xét ΔHCB vuông tại H và ΔFAC vuông tại F có
góc HCB=góc FAC
=>ΔHCB đồng dạng với ΔFAC
=>CH/AF=CB/CA
=>CH*CA=CB*AF=AD*AF
=>AB*AE+AD*AF=AC^2
Đúng 1
Bình luận (0)
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF
A
C
2
Đọc tiếp
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF = A C 2
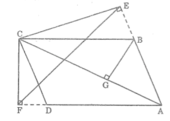
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: 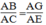
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: 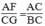 ⇒ BC.AF = AC.CG
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD,AC>BD, CE vuông góc với AB (E thuộc AB). CF vuông góc với AD(F thuộc AD).
Chứng minh rằng AB.AE+AD.AF=AC2.
Ta chứng minh

Tương tự câu a ta chứng minh được

Þ AD.AF =AK.AC (2)
Từ (1) ta có AB.AE = AC.AH (3)
Lấy (3) + (2) ta được AD.AF + AB.AE = AC2 (ĐPCM)
Cho hình bình hành ABCD (AC>BD). Vẽ CE vuông góc vói AB, CF vuông góc với AD
A) vẽ BH vuông góc AC tại H. Chứng minh tam giác ABH~tam giác ACE và AB.AE=AC.AH
B) chứng minh tam giác CBH~tam giác ACF và AB. AE+AD.AF=AC2
a. hai tg ABG và tg ACE vuông tại G và E có góc GAB chung nên đồng dạng(gg)
b. Vì tg AEC và ABG đồng dạng --> AB/AC = AG/AE -> AB.AE = AC.AG(1)
Vì hai tg vuông AFC và CGB có góc CAF = góc BCG (slt) --> tg AFC và tg CGB đồng dạng --> AF/CG = AC/BC --> AF.BC = AC.CG thay BC = AD --> AF.AD = AC.CG (2).
Cộng (1) và (2) vế theo vế --> AB.AE + AD.AF = AC.AG + AC.CG = AC(AG+GC) = AC.AC = AC^2
Vậy AB.AE + AD.AF = AC^2.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Kẻ CE vuông góc với đg thẳng AB tại E, kẻ CF vuông góc với đg thẳng AD tại F. CM: AC2 = AB.AE+AD.AF
















