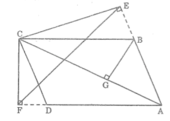
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: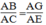 
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: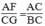 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2
Giả sử AC là đường chéo lớn của tứ giác ABCD. Từ C vẽ đường thẳng CE vuông góc với AB, đường thẳng CF vuông góc với AD (EF thuộc phần kéo dài của phần AB,AD)
CMR: AB.AE+AD.AF=AC^2
Bài tập: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C kẻ đường vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB, AD). Chứng minh: AB . AE + AD . AF = AC2
- Bài này khó, bạn làm biết làm thì giúp mình nhé. Cám ơn nhìu!
Cho hình bình hành ABCD (AB > AD). Từ C vẽ CE, CF lần lượt vuông góc với các đường thẳng AB, AD (E thuộc AB, F thuộc AD). Chứng minh rằng AB.AE + AD.AF = AC2.
Cho hình bình hành ABCD có Ac là đường chéo lớn. Từ C kẻ CE vuông góc với đường thẳng Ab (E\(\in\)AB) và kẻ CF vuông góc với đường thẳng AD (F\(\in\)AD). Chứng minh \(AB.AE+AD.AF=AC^2\)
Cho hình bình hành ABCD ( AB > AD) Từ C kẻ CE và CF vuông góc với đường thẳng AB , AD ( E thuộc AB , F thuộc AD) . Chứng minh
AB.AE + AD.AF = AC^2
cho hình bình hành ABCD có đường chéo AC là lớn nhất .từ C hạ các đường vuông góc CE và CF lần lượt xuống các tia AB,AD .chứng minh rằng AB.AE+AD.AF=AC2
Cho hình bình hành ABCD với đường chéo AC>BD. Gọi E và F lần lượt là chân đường vuông góc kẻ từ C đến các đường thẳng AB và AD; gọi G là chân đường vuông góc kẻ từ B đến AC.
a) Chứng minh rằng 2 tam giác CBG và ACF đồng dạng
b)Chứng minh rằng: AB.AE +AD.AF=AC2
Cho AC là đường chéo lớn của hình bình hành ABCD. Từ C kẻ CE vuông góc với AB, kẻ CF vuông góc với AD (E,F thuộc AB và AD). Chứng minh rằng: AB*AE+AD*AF=AC2
cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD. Gọi E,F lần lượt là chân đường vg góc kẻ từ C đến các đg thẳng AB,AD. G là chân đường vg góc kẻ từB đến AC Chứng minh rằng:
a)tam giác BCG ∼tam giác CAF
b) AB.AE+AD.AF=AC2
