chứng minh vô nghiệm
x4-2x3+5x2-4x+3
giúp em với ạ
2x3 + 5x2 - 3x = 0
Giúp em với ạ
\(2x^3+5x^2-3x=0\)
\(\Leftrightarrow x\left(2x^2+5x-3\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
chứng minh rằng số dư của a khi chia cho 3 bằng số dư tổng các chữ số của a khi chia cho 3
GIÚP EM VỚI Ạ
Cứu với ạ
Làm tính chia
1) (x3 – 3x2 + x – 3) : (x – 3) 2) (2x4 – 5x2 + x3 – 3 – 3x) : (x2 – 3)
3) (x – y – z)5 : (x – y – z)3 4) (x2 + 2x + x2 – 4) : (x + 2)
| 5) (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1) | 6) (2x3 – 5x2 + 6x – 15):(2x – 5) |
A= 1- 4x2/ 2+ 4x: 2- 4x/ 3
Giúp mik với ạ!
\(A=\dfrac{\left(1-2x\right)\left(1+2x\right)}{2\left(1+2x\right)}:\dfrac{2\left(1-2x\right)}{3}\)
\(=\dfrac{1-2x}{2}\cdot\dfrac{3}{2\left(1-2x\right)}=\dfrac{3}{4}\)
Tìm bậc của mỗi đa thức sau
a) f (x) = 3x2 + 2x3 - 6x - 2
b) g(x) = 5x2 + 9 - 2x3 - 3x2 - 4x + 2x3 - 2
f (x) = 3x2 + 2x3 - 6x - 2
bậc của đa thức là: 3
g(x) = 5x2 + 9 - 2x3 - 3x2 - 4x + 2x3 - 2
g(x) = ( 5x2 - 3x2 ) + ( 9 -2) + ( - 2x3 + 2x3 ) - 4x
g(x) = 2x2 + 7 - 4x
bậc của đa thức là : 2
Chứng minh rằng phương trình sau có ít nhất hai nghiệm: 2 x 3 - 5 x 2 + x + 1 = 0
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
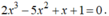
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
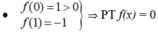 có ít nhất một nghiệm c1 ∈ (0;1).
có ít nhất một nghiệm c1 ∈ (0;1).
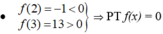 có ít nhất một nghiệm c2 ∈ (2;3).
có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.
Bài 5:
1) a) Cho hai đa thức:
P (x) = 5x2 + 3x3 - 5x2 + 2x3 – 2 +4x – 4x2 + x3
Q(x) = 6x – x3 + 5 – 4x3 + 6 – 3x2 – 7x2
Tính M(x) = P(x) + Q(x)
b) Tìm C(x) biết: (5x2 + 9x – 3x4 + 7x3 -12) + C(x) = -2x3 + 9 – 6x + 7x4 -2x3
2) Tìm nghiệm của các đa thức sau
a) 4x - ![]() b) x2 – 4x +3
b) x2 – 4x +3
a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21
x^2+4x+5=2√2x+3
giúp mình với ạ
\(x^2+4x+5=2\sqrt{2x+3}\)
\(ĐK:x\ge-\dfrac{3}{2}\)
\(pt\Leftrightarrow(2x+3-2\sqrt{2x+3}+1)+x^2+2x+1=0\)
\(\Leftrightarrow\left(\sqrt{2x+3}-1\right)^2=-\left(x+1\right)^2\)
Vì \(\left(\sqrt{2x+3}-1\right)^2\ge0;-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}(\sqrt{2x+3}-1)^2=0\\\left(x+1\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2x+3}-1=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2x+3}=1\\x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3=1\\x=-1\end{matrix}\right.\Leftrightarrow x=-1\left(tm\right)}\)
\(\Leftrightarrow x=-1\left(tm\right)\)
Vậy, pt có nghiệm duy nhất là x=-1
Phân tích đa thức thành nhân tử
2x3+5x2+4x-2