a) Vì u+v=29 và uv=198 nên u,v là hai nghiệm của phương trình:

\(x^2-29x+198=0\)

\(\Leftrightarrow x^2-18x-11x+198=0\)

\(\Leftrightarrow x\left(x-18\right)-11\left(x-18\right)=0\)

\(\Leftrightarrow\left(x-18\right)\left(x-11\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-18=0\\x-11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=18\\x=11\end{matrix}\right.\)

Vậy: u=18; v=11

a) Vì \(u+v=3\sqrt{2}\) và uv=4

nên u,v là hai nghiệm của phương trình: \(x^2-3\sqrt{2}x+4=0\)

\(\Delta=\left(-3\sqrt{2}\right)^2-4\cdot1\cdot4=18-16=2>0\)

Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{3\sqrt{2}-\sqrt{2}}{2}=\sqrt{2}\\x_2=\dfrac{3\sqrt{2}+\sqrt{2}}{2}=2\sqrt{2}\end{matrix}\right.\)

Vậy: \(u=\sqrt{2};v=2\sqrt{2}\)

a) S = 42; P = 441  ⇒   S 2   –   4 P   =   42 2   –   4 . 441   =   0

⇒ u và v là hai nghiệm của phương trình:  x 2   –   42 x   +   441   =   0

Có:   Δ ’   =   ( - 21 ) 2   –   441   =   0

⇒ Phương trình có nghiệm kép  x 1   =   x 2   =   - b ’ / a   =   21 .

Vậy u = v = 21.

b) S = -42; P = -400  ⇒   S 2   –   4 P   =   ( - 42 ) 2   –   4 . ( - 400 )   =   3364   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   42 x   –   400   =   0

Có  Δ ’   =   21 2   –   1 . ( - 400 )   =   841

⇒ Phương trình có hai nghiệm phân biệt:

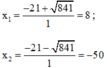
Vậy u = 8; v = -50 hoặc u = -50; v = 8.

c) u – v = 5 ⇒ u + (-v) = 5

u.v = 24 ⇒ u.(-v) = -uv = -24.

Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

S= u + (-v) = 5; P = u. (-v) = -24 ⇒  S 2   –   4 P   =   5 2   –   4 . ( - 24 )   =   121   >   0

⇒ u và –v là hai nghiệm của phương trình:  x 2   –   5 x   –   24   =   0

Có  Δ   =   ( - 5 ) 2   –   4 . 1 . ( - 24 )   =   121

⇒ Phương trình có hai nghiệm phân biệt

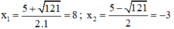
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8

⇒ u = 8; v = 3 hoặc u = -3; v = -8.

S = 42; P = 441 ⇒ S2 – 4P = 422 – 4.441 = 0

⇒ u và v là hai nghiệm của phương trình: x2 – 42x + 441 = 0

Có: Δ’ = (-21)2 – 441 = 0

⇒ Phương trình có nghiệm kép x1 = x2 = -b’/a = 21.

Vậy u = v = 21.

a) u + v = 42, uv = 441 => u, v là nghiệm của phương trình:

x² – 42x + 441 = 0

∆’ = 21² – 441 = 441 – 441 = 0, √∆’ = 0; x₁ = x₂ = 21

Vậy u = v = 21

b) u + v = -42, uv = -400, u, v là nghiệm của phương trình:

x² + 42x – 400 = 0

∆’ = 441 + 400 = 841, √∆’ = 29; x₁ = 8, x₂ = -50. Do đó:

u = 8, v = -50 hoặc u = -50, v = 8

c) u – v = 5, uv = 24. Đặt –v = t, ta có u + t = 5, ut = -24, ta tìm được:

u = 8, t = -3 hoặc u = -3, t = 8. Do đó:

u = 8, v = 3 hoặc u = -3, t = 8.

a) u + v = 42, uv = 441 => u, v là nghiệm của phương trình:

x2 – 42x + 441 = 0

∆’ = 212 – 441 = 441 – 441 = 0, √∆’ = 0; x1 = x2 = 21

Vậy u = v = 21

b) u + v = -42, uv = -400, u, v là nghiệm của phương trình:

x2 + 42x – 400 = 0

∆’ = 441 + 400 = 841, √∆’ = 29; x1 = 8, x2 = -50. Do đó:

u = 8, v = -50 hoặc u = -50, v = 8

c) u – v = 5, uv = 24. Đặt –v = t, ta có u + t = 5, ut = -24, ta tìm được:

u = 8, t = -3 hoặc u = -3, t = 8. Do đó:

u = 8, v = 3 hoặc u = -3, t = 8.

a) u, v là nghiệm phương trình: 

X^2 - 15 X + 36 = 0 

\(\Delta=15^2-4.36=81\)

=> \(\orbr{\begin{cases}X=\frac{-\left(-15\right)+\sqrt{81}}{2}=12\\X=\frac{-\left(-15\right)-\sqrt{81}}{2}=3\end{cases}}\)

Vậy (u; v) = ( 12; 3 ) hoặc (u; v ) = (3; 12) 

b) và c ) tương tự 

d) \(u^2+v^2=\left(u+v\right)^2-2uv=13\)

=> \(\left(u+v\right)^2=25\)

=> u + v = 5 hoặc u + v = - 25 

Có 2 TH: 

TH1: u + v = 5 và uv= 6 

TH2: u + v = -5 và uv = 6 

Làm tương tự như câu a.