Cho M=3x+x2-y2/x2+1
N=(x+1)2+(y-√2)2+2016
Tính giá trị của M tại x, y thỏa mãn N đạt giá trị nn
Những câu hỏi liên quan
11 tháng 1 2022 lúc 20:02
Cho hệ phương trình \(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\) (với m là tham số)
Tìm m để hệ đã cho có nghiệm (x;y) thỏa mãn: x2 + y2 + 3 đạt giá trị nhỏ nhất.
\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y+x+2y=4m-2+3m+2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\m+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\2y=2m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)
\(x^2+y^2+3\\ =m^2+\left(m+1\right)^2+3\\ =m^2+m^2+2m+1+3\\ =2m^2+2m+4\\ =2\left(m^2+m+2\right)\)
\(=2\left(m^2+m+\dfrac{1}{4}+\dfrac{7}{4}\right)\)
\(=2\left[\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\right]\)
\(=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...
Đúng 1
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Tìm các giá trị của tham số m để hàm số:
y
1
3
m
x
3
-
(
m
-
1
)
x
2
+
3
(
m
-
2
)
x
+...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số: y = 1 3 m x 3 - ( m - 1 ) x 2 + 3 ( m - 2 ) x + 1 6 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1
A. 1 - 6 2 < m < 1 + 6 2 .
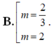
C. m ∈ 1 - 6 2 ; 1 + 6 2 \ 0 .
D. m = 2 .
Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1
Đúng 0
Bình luận (0)
Cho x , y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
2...
Đọc tiếp
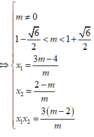
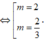
Cho x , y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y . Khi đó, giá trị của M+m bằng.
A. 41
B. 42
C. 43
D. 44
Cho Parabol (P: y=x^2 và (d): y= 3x+ m^2 *-1 (với m là tham số) đường thẳngTìm tất cả các giá trị của tham số m để đường thẳng cắt Parabol tại hai điểm phân biệt A(x1 ,y1) B (x2, y2) sao cho x1,y1 thỏa mãn |x1|+2 |x2| = 3 : .
PTHĐGĐ là;
x^2-3x-m^2+1=0
Δ=(-3)^2-4(-m^2+1)=4m^2-4+9=4m^2+5>0
=>Phương trình luôn có hai nghiệm phân biệt
TH1: x1>0; x2>0
=>x1+2x2=3
mà x1+x2=3
nên x1=1; x2=1
x1*x2=-m^2+1
=>-m^2+1=1
=>m=0
TH2: x1<0; x2>0
=>-x1+2x2=3 và x1+x2=3
=>x1=1; x2=2
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2-1=0(loại)
TH2: x1>0; x2<0
=>x1-2x2=0 va x1+x2=3
=>x1=2 và x2=1
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2=1(loại)
TH3: x1<0; x2<0
=>-x1-2x2=3 và x1+x2=3
=>x1=9 và x2=-6
x1*x2=-m^2+1
=>-m^2+1=-54
=>-m^2=-55
=>\(m=\pm\sqrt{55}\)
Đúng 0
Bình luận (1)
tìm tất cả các giá trị của m sao cho hai parabol y=x^2+mx+(m+1)^2 và y=-x^2-(m+2)x-2(m+1) cắt nhau tại 2 điểm có hoành độ lần lượt là x1,x2 thỏa mãn P=|x1x2-3(x1+x2)| đạt GTLN
Phương trình hoành độ giao điểm là:
\(x^2+mx+\left(m+1\right)^2=-x^2-\left(m+2\right)x-2\left(m+1\right)\)
=>\(x^2+mx+\left(m+1\right)^2+x^2+\left(m+2\right)x+2m+2=0\)
=>\(2x^2+\left(2m+2\right)x+\left(m^2+4m+3\right)=0\)
\(\Delta=\left(2m+2\right)^2-4\cdot2\cdot\left(m^2+4m+3\right)\)
\(=4m^2+16m+16-8m^2-32m-24\)
\(=-4m^2-16m-8=-4\left(m^2+4m+2\right)\)
\(=-4\left(m^2+4m+4-2\right)\)
\(=-4\left[\left(m+2\right)^2-2\right]\)
Để (P1) cắt (P2) tại hai điểm thì \(\Delta>=0\)
=>\(\left(m+2\right)^2-2< =0\)
=>\(\left(m+2\right)^2< =2\)
=>\(-\sqrt{2}< =m+2< =\sqrt{2}\)
=>\(-\sqrt{2}-2< =m< =\sqrt{2}-2\)
\(P=\left|x_1\cdot x_2-3\left(x_1+x_2\right)\right|\)
\(=\left|\dfrac{m^2+4m+3}{2}-3\cdot\dfrac{-2m-2}{2}\right|\)
\(=\left|\dfrac{m^2+4m+3+6m+6}{2}\right|=\left|\dfrac{m^2+10m+9}{2}\right|>=0\)
Dấu '=' xảy ra khi |m2+10m+9|=0
=>(m+1)(m+9)=0
=>\(\left[{}\begin{matrix}m=-1\left(nhận\right)\\m=-9\left(loại\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm tất các giá trị thực của tham số m để hàm số
y
1
3
x
3
+
(
m
+
3
)
x
2
+
4
(
m
+
3
)
x
+
m
3...
Đọc tiếp
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn -2< x 1 < x 2
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
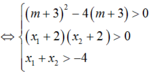
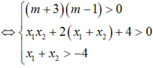
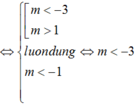
Chọn C
Đúng 0
Bình luận (0)
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Cho hai số thực x;y thỏa mãn
x
2
+
y
2
≥
9
và
log
x
2
+
y
2
x
8
x
2
+...
Đọc tiếp
Cho hai số thực x;y thỏa mãn x 2 + y 2 ≥ 9 và log x 2 + y 2 x 8 x 2 + 8 y 2 - 7 x - 7 y 2 ≥ 2 . Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=3x+y lần lượt là M và m. Khi đó giá trị của biểu thức M + 2m bằng
