Cho tam giác ABC vuông tại A có AB=3cm,AC=8 cm . Kẻ AH vuông góc BC . Tính BH,HC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=6cm,AC=8 cm . Kẻ AH vuông góc BC . Tính BC, AH,BH,HC
Ap dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Đúng 0
Bình luận (0)
Ta có hình vẽ:
Áp dụng định lý Pitago. Ta có:
BC2 = AB2 + AC2 <=> 62 + 82 = 100 cm2
100 = 10 x 10
=> BC = 10 cm
Áp dụng công thức Heron để tính chiều cao. Ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)
Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm
Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)
Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao
2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)
\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)
Độ dài cạnh BH là: (Bạn tự làm)
Độ dài cạnh HC là: (Bạn tự làm nhé)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=3cm,BC=4cm,AC=5cm.a,CM tam giác ABC là tam giác vuông.b,Kẻ BH vuông góc AC tại H.Biết 16AH=9HC.Tính BH,HC,AH
a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
Đúng 0
Bình luận (0)
1, Tam giác ABC vuông tại A, kẻ đường cao AH
a.Tính AB, AC,BC, HC nếu AH= 6cm, BH= 4,5cm
b.Biết AB= 6cm, HB- 3cm. Tính AH, AC,CH
5, Cho tam giác ABC vuông tại A có AB=21cm, góc C= 40 độ
a.Tính AC
b,Tính BC
Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AC 20 cm. Kẻ AH vuông góc với BC. Biết BH 9cm, HC 16 cm. Tính độ dài cạnh AB, AH? A.
A
H
12
c
m
;
A
B
15
c
m
B.
A
H
10
c
m
;
A
B
15
c
m
C.
A
H
15
c
m
;
A...
Đọc tiếp
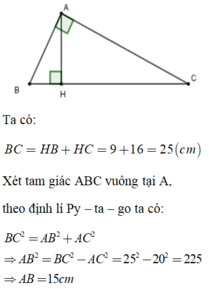
Cho tam giác ABC vuông tại A có AC = 20 cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16 cm. Tính độ dài cạnh AB, AH?
A. A H = 12 c m ; A B = 15 c m
B. A H = 10 c m ; A B = 15 c m
C. A H = 15 c m ; A B = 12 c m
D. A H = 12 c m ; A B = 13 c m
1Cho tam giác ABC cân tại A. Kẻ BH vuông với AC biết AH= 6cm HC= 3cm. Tính BC
2 Cho tam giác ABC vuông tại A có góc B=60độ CMR AB=1/2BC
Lê Xuân Trường
1-Xét tam giác ABH và tam giác ACH có
Góc AHB = Góc AHC = 90 độ
AC = AB (Do tam giác ABC cân tại A)
Góc ABH = Góc ACH(Do tam giác ABC cân tại A)
Suy ra tam giác ABH = tam giác ACH (cạnh huyền -góc nhọn )
Suy ra BH = CH =3 cm (2 cạnh tương ứng )
2 . Tui không biết làm thông cảm nhe !
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH a, Biết AH = 6 cm , BH = 4,5 cm . Tính AB , AC , BC, HC b, Biết AB=6 cm , BH = 3cm . Tính AH , AC ,HC
cho tam giác vuông tại a có ac = 20 cm kẻ ah vuông góc bc tại h biết bh= 9 cm ,hc= 16 cm . tính ab , ah ?
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=AC^2-HC^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm
Đúng 2
Bình luận (0)
Vì AH⊥BC => △ABH và △ACH vuông tại H Áp dụng định lý Pi-ta-go vào △ABH và △ACH, ta có:
AC2=AH2+CH2
=>AH2=AC2-CH2
AH2=202- 162
AH2= 144 => AH= căn bậc hai của 144= 12 (cm)
AB2=AH2+BH2
AB2= 122+92
AB2= 144+81
AB2= 225 => AB= căn bậc hai của 225 =15 (cm)
Vậy AB = 15 cm, AH = 12 cm
Đúng 1
Bình luận (0)
1.Cho tam giác ABC từ A kẻ AH vuống góc với BC tại H.Biết AH=6 cm, BH=4,5 cm, HC=8 cm.
a)Tính AB và AC
b)Chứng tỏ tam giác ABC là tam giác vuông.
Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC. Biết AH=7cm, HC=3cm. Tính BC
\(\Rightarrow AC=10cm\)
\(\Rightarrow AB=10cm\) ( AB = AC )
Áp dụng định lý pitago vào tam giác vuông ABH
\(AB^2=AH^2+HB^2\)
\(\Rightarrow HB=\sqrt{AB^2-AH^2}=\sqrt{10^2-7^2}=\sqrt{51}\)
Áp dụng định lí pitago vào tam giác vuông BHC
\(BC^2=HC^2+HB^2\)
\(\Rightarrow BC=\sqrt{3^2+\sqrt{51}^2}=2\sqrt{15}\)
Đúng 0
Bình luận (0)