cho tam giác ABC có các cạnh thỏa mãn hệ thức ( a+b+c )( a+b−c ) =3ab .tìm số đo góc C

Những câu hỏi liên quan
Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
Chọn B.
Ta có:
a(a2 – c2) = b(b2 – c2) ⇔ a3 – ac2 = b3 – bc2
⇔ a3 – b3 = ac2 – bc2
⇔ (a – b)(a2 + ab + b2) = c2(a – b)
⇔ a2 + ab + b2 = c2
⇔ ab = c2 – a2 – b2
Ta lại có: 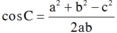
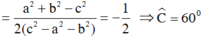
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh BC=a, AC=b, AB=c thỏa mãn \(a^4+b^4+c^4=2a^2b^2+2a^2c^2\). Tìm số đo góc \(\widehat{BAC}\)
Giả thiết tương đương:
\(a^4+b^4+c^4+2b^2c^2=2a^2\left(b^2+c^2\right)+2b^2c^2\)
\(\Leftrightarrow a^4+\left(b^2+c^2\right)^2=2a^2\left(b^2+c^2\right)+2b^2c^2\)
\(\Leftrightarrow\left(b^2+c^2-a^2\right)^2=2b^2c^2\)
\(\Leftrightarrow b^2+c^2-a^2=\pm\sqrt{2}bc\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{\pm\sqrt{2}bc}{2bc}=\pm\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}A=45^0\\A=135^0\end{matrix}\right.\)
Đúng 1
Bình luận (1)
cho tam giác ABC có BC=a CA=b AB=c, thỏa mãn (a+b+c)(a+b-c)=3ab. Tìm độ lớn góc C?
\(\left(a+b+c\right)\left(a+b-c\right)=3ab\)
\(\Leftrightarrow\left(a+b\right)^2-c^2=3ab\)
\(\Leftrightarrow a^2+b^2+2ab-c^2=3ab\)
\(\Leftrightarrow a^2+b^2-c^2=ab\)
\(\Leftrightarrow\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{1}{2}\)
\(\Rightarrow cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{1}{2}\)
\(\Rightarrow C=60^0\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có BC = a, CA = b và AB = c thỏa mãn hệ thức : \(\dfrac{c}{b+a}+\dfrac{b}{a+c}=1\). Hãy tính số đo của góc A ?
cho tam giác ABC vuông tại A, có độ dài của các cạnh thỏa mãn hệ thức: BC^2 = (căn 3 + 1)AC^2 + ( căn 3 - 1 ) AB.AC. Tính số đo góc ABC
Cho tam giác có số đo một góc bằng trung bình cộng của số đo hai góc còn lại và độ dài các cạnh a,b,c của tam giác đó thỏa mãn:\(\sqrt{a+b-c}=\sqrt{a}+\sqrt{b}-\sqrt{c}\)
Tam giác này là tam giác gì? Vì sao?
Cho a,b,c là độ dài 3 cạnh của tam giác ABC thỏa mãn hệ thức: a³ + b³ + c³ = 3abc. Hỏi tam giác ABC là tam giác gì?
\(a^3-b^3-c^3=3abc\)
\(\Rightarrow a^3-b^3-c^3-3abc=0\)
\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
Mà \(a+b+c\ne0\) (độ dài 3 cạnh của 1 tam giác)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ac=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow\left(a-b\right)^2=0;\left(b-c\right)^2=0;\left(c-a\right)^2=0\)
\(\Rightarrow a=b=c\)
Do đó tam giác ABC là tam giác đều
Đúng 0
Bình luận (0)
Các bạn ơi giải bài toán này giúp mình với nhé !Bài 1 :a) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ thận với 3 , 11 , 16 . Tìm số đo các góc của tam giác ABC .b) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ nghịch với 15 , 16 , 48 . Tìm số đo các góc của tam giác ABC .c) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ thuân với 5 , 7 , 8 . Tìm số đo các góc của tam giác ABC.d) Cho tam giác ABC cósố đo ba góc A , B , C tỉ lệ nghịch với 4 , 4, 3 . Tìm số đo các gọc của tam giác ABC .m...
Đọc tiếp
Các bạn ơi giải bài toán này giúp mình với nhé !
Bài 1 :
a) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ thận với 3 , 11 , 16 . Tìm số đo các góc của tam giác ABC .
b) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ nghịch với 15 , 16 , 48 . Tìm số đo các góc của tam giác ABC .
c) Cho tam giác ABC có số đo ba góc A , B , C tỉ lệ thuân với 5 , 7 , 8 . Tìm số đo các góc của tam giác ABC.
d) Cho tam giác ABC cósố đo ba góc A , B , C tỉ lệ nghịch với 4 , 4, 3 . Tìm số đo các gọc của tam giác ABC .
mình rất cần bài này để chuẩn bị đi học !
bài này lóp 7 hoc rù nhung quyen lop 7 nhình học giỏi lám đó
Đúng 0
Bình luận (0)
1.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ nghịch vs 3;4;6.Tính số đo các góc của tam giác ABC.
2.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ thuận vs 3;4;5.Tính số đo các góc của tam giác ABC.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có số đo 3 góc là A, B, C thỏa mãn điều kiện \(\tan\dfrac{A}{2}+\tan\dfrac{B}{2}+\tan\dfrac{C}{2}=\sqrt{3}\) . Tam giác ABC là tam giác gì ?
\(\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow tan\dfrac{A}{2}.tan\dfrac{C}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Ta có:
\(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\ge\sqrt{3\left(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}\right)}=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(A=B=C\) hay tam giác ABC đều
Đúng 2
Bình luận (0)




















