cho tứ giác abcd(ab//dc,ab<dc) cm: ad=be,ab=de;dc-ab=ec;ad+bc>dc-ab
Những câu hỏi liên quan
cho tứ giác abcd có ab+dc+ac=10cm. tính đường chéo bd biết diện tích tứ giác abcd đạt gtln
Cho tứ giác ABCD. Nếu
A
B
→
D
C
→
và
A
C
→
B
C
→
thì ABCD là: A. Hình bình hành B. Hình vuông C. Hình chữ nhật D. Hình thoi
Đọc tiếp
Cho tứ giác ABCD. Nếu A B → = D C → và A C → = B C → thì ABCD là:
A. Hình bình hành
B. Hình vuông
C. Hình chữ nhật
D. Hình thoi
Tứ giác ABCD là hình gì nếu A B → = D C → v à A B → = D C →
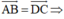tứ giác ABCD là hình bình hành
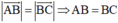
⇒ tứ giác ABCD là hình thoi.
(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)
Đúng 0
Bình luận (0)
cho tứ giác ABCD có AB = DC gọi M, N , P lần lượt là trung điểm của AB, BD, DC . CMR : tam giác MNP là tam giác cân
- Cho tứ giác ABCD có AB + BD < AC + DC. CMR : AB < AC
Cho tứ giác ABCD, AB+BD không lớn hơn AC+DC. CMR AB<AC
AB+BD\(\le\)AC+DC
=> AC - AB\(\ge\) BD-DC ma BD>CD ( Tu giac loi co duong cheo > canh)
=> AC-AB> hay AC> AB
Đúng 0
Bình luận (0)
Gọi O là giao điểm của AC và BD.
Theo định lí Pytago trong các tam giác: △AOB, △COD△AOB, △COD ta có
AB<AO+BO
CD<CO+DO
→AB+CD<AC+BD
Mà AB+BD\(\le\)AC+CD
→2AB+CD+BD<2AC+CD+BD
→AB<AC
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có AB=AD=DC/2.Góc A=90°.BE vuông góc với DC tại E.
a,Tứ giác ABED là hình gì?
b,Tứ giác ABCE la hình gì?
c,Cho AB=4cm.Tính diện tích tứ giác ABCD và diện tích ABC?
Giúp với mai thi rồi.(ý b,c)
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \)
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Đúng 1
Bình luận (0)
cho tứ giác ABCD, có góc ngoài của tứ giác tại đỉnh C bàng ACB. cmr AB+BD>AC+DC