Giải tam giác vuông abc, góc a=90 độ. Ac= 21cm;ab=18cm

Những câu hỏi liên quan
giải tam giác vuông ABC,biết góc A=90 độ và a)b=15cm,góc C=30 độ
b)b=21cm,c=18cm
nhớ vẽ cả hình của 2 phần
tui lạy chủ của câu hỏi này
https://hoc24.vn/cau-hoi/cau-rut-gon-thuong-duoc-su-dung-trong-cac-the-loai-nao.246303383406?utm_source=dable
Đúng 0
Bình luận (0)
a: Ta có: ΔABC vuông tại A
nên \(\widehat{C}+\widehat{B}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=15\cdot\dfrac{\sqrt{3}}{3}\)
\(=5\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=15^2+\left(5\sqrt{3}\right)^2=300\)
hay \(BC=10\sqrt{3}\left(cm\right)\)
Đúng 3
Bình luận (1)
Xem thêm câu trả lời
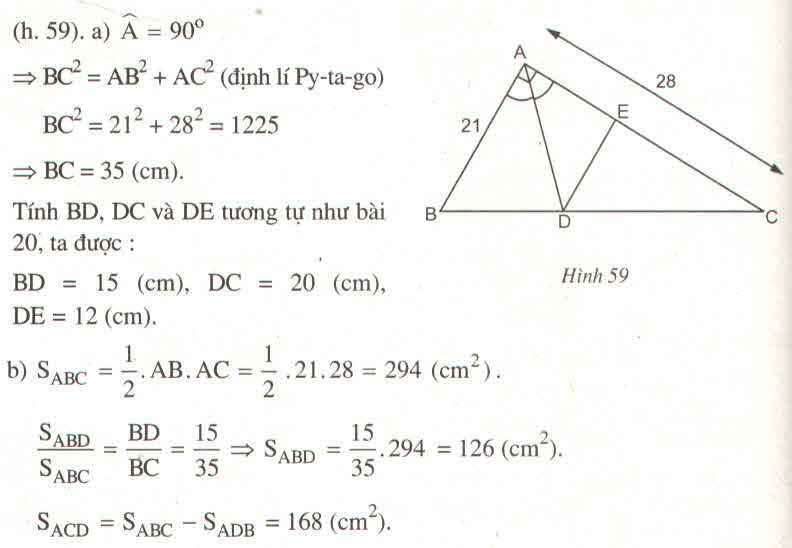
.cho tam giác vuông ABC ( góc A= 90 độ) AB=28cm, AC=21cm đường phân giác góc A cắt BC tại D đường thẳng qua D và song song với AC, cắt AB tại E.
a) tính BD, BC và DE
bài 2 . Giải tam giác vuông ABC , biết góc A =90 độ và
a. a=72cm, góc B=58 độ
b. b=20cm, góc B=40 độ
c. b=15cm, góc C=30 độ
a. b=21cm, c=18cm
a.
$\widehat{C}=90^0-\widehat{B}=90^0-58^0=32^0$
$\cos B=\frac{c}{a}\Rightarrow c=a\cos B=72\cos 58^0=38,15$ (cm)
$\sin B=\frac{b}{a}\Rightarrow b=a\sin B=72\sin 58^0=61,06$ (cm)
b.
$\widehat{C}=90^0-\widehat{B}=90^0-40^0=50^0$
$\sin B=\frac{b}{a}\Rightarrow a=\frac{b}{\sin B}=\frac{20}{\sin 40^0}=31,11^0$
$\tan B=\frac{b}{c}\Rightarrow c=\frac{20}{\tan 40^0}=23,84^0$
Đúng 1
Bình luận (3)
c.
$\widehat{B}=90^0-\widehat{C}=90^0-30^0=60^0$
$\tan B=\frac{b}{c}\Rightarrow c=\frac{b}{\tan B}=\frac{15}{\tan 60^0}=5\sqrt{3}$ (cm)
$\sin B=\frac{b}{a}\Rightarrow a=\frac{b}{\sin B}=\frac{15}{\sin 60^0}=10\sqrt{3}$ (cm)
d
$a=\sqrt{b^2+c^2}=\sqrt{21^2+18^2}=3\sqrt{85}$ (cm)
$\tan B=\frac{b}{c}=\frac{21}{18}=\frac{7}{6}$
$\Rightarrow \widehat{B}=49,4^0$
$\widehat{C}=90^0-\widehat{B}=40,6^0$
Đúng 1
Bình luận (0)
a, giải △ABC vuông ở A biết AB= 3, AC= 7
b, giải tam giác vuông ABC ( góc A= 90 độ) biết BC= 14, góc B = 42 độ
mọi người cứu em với
Cho tam giác ABC vuông tại A. Giải tam giác ABC biết AB= 21cm, góc C =42 độ
\(\widehat{B}=48^0\)
\(BC\simeq31,38\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A(góc A=90°),AB=21cm,AC=28cm. Vẽ đường cao AH(H thuộc BC). Tia phân giác của góc A cắt BC tại D. Tính BC,BD,CD và diện tích tam giác AHD
Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(=21^2+28^2\)
\(=1225\)
->\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là tia phân giác ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)
⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)
⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A,AB=21cm,góc C=40 độ .Tính
a,AC,BC b,Phân giác BD
a) Ta có:
\(sin40=\dfrac{AB}{BC}=\dfrac{21}{BC}\)\(\Rightarrow BC=\dfrac{21}{sin40}\simeq33cm\)
\(cos40=\dfrac{AC}{BC}\Rightarrow AC=cos40.33\simeq25cm\)
b) \(sinB=\dfrac{AC}{BC}=\dfrac{25}{33}\Rightarrow\widehat{B}\simeq49^o\)
\(BD=\dfrac{2.BC.AB.cos24,5}{BC+AB}\simeq12cm\)
Đúng 2
Bình luận (0)
\(Taco.\dfrac{BC}{sinA}=\dfrac{AB}{SinC}\Rightarrow BC=32,67cm=>AC=\sqrt{32,67^2-21^2}=25cm\)
Taco ^B=90-40=30 do
\(BD=\dfrac{2.21.32,67}{21+32,67}.CosB:2=24,69cm\)
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: AC
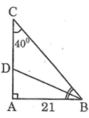
Cho tam giác ABC góc A= 90 độ; góc B= 37 độ; BC= 10cm.
a) Giải tam giác vuông.
b) Kẻ AH vuông góc với BC; H thuộc BC; HE vuông góc với AC; E thuộc AC.
c) Tính diện tích AEH?