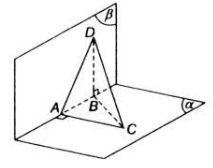
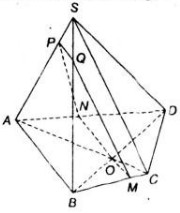
Trên mặt phẳng \(\left(\alpha\right)\) cho hình bình hàng ABCD. Gọi O là giao điểm của AC và BD, S là một điểm nằm ngoài mặt phẳng \(\left(\alpha\right)\) sao cho SA = SC; SB = SD. Chứng minh rằng :
a) \(SO\perp\left(\alpha\right)\)
b) Nếu trong mặt phẳng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc với mặt phẳng (SOH)