từ điểm M nằm ngoài (O;R) vẽ tiếp tuyến MA,MB và cát tuyến MCD (cắt đoạn OB). AB cắt MO,CD lần lượt tại H,E. Gọi K là trung điểm CD
a, c/m MAOB nội tiếp;OHEK nội tiếp
b, c/m MC*MD=ME*MK

Những câu hỏi liên quan
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minha, Tứ giác OAMC nội tiếpb, K là trung điểm của BDc, AC là phân giác của góc BHD
Đọc tiếp
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minh
a, Tứ giác OAMC nội tiếp
b, K là trung điểm của BD
c, AC là phân giác của góc BHD
a) Xét tứ giác OAMC có
\(\widehat{OAM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OAMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minha, Tứ giác OAMC nội tiếpb, K là trung điểm của BDc, AC là phân giác của góc BHD
Đọc tiếp
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minh
a, Tứ giác OAMC nội tiếp
b, K là trung điểm của BD
c, AC là phân giác của góc BHD
a: góc OAM+góc OCM=180 độ
=>OAMC nội tiếp
b: CE//BD
=>góc AKM=góc AEC=góc ACM
=>AKCM nội tiếp
=>A,K,C,M cùng nằm trên 1 đường tròn
=>góc OKM=90 độ
=>K là trung điểm của BD
Đúng 0
Bình luận (0)
Trên một đường thẳng lấy ba điểm M, N, O trong đó O nằm giữa M và N. Từ điểm A nằm ngoài đường thẳng này vẽ các tia AM, AN, AO. Lấy điểm B nằm giữa O và A. Tia MB cắt tia AN tại C. Giải thích vì sao điểm C nằm giữa A và N.
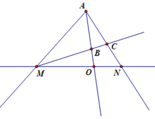
Tia MB cắt đoạn thẳng AO tại điểm B nằm giữa A và O nên tia MB nằm giữa hai tia MA, MO (hay tia MB nằm giữa hai tia MA, MN).
Vì tia MB nằm giữa hai tia MA, MN nên tia MB cắt đoạn thẳng AN tại điểm C nằm giữa hai điểm A, N.
Vậy tia MB cắt tia AN tại điểm C nằm giữa A, N.
Đúng 0
Bình luận (0)
Từ điểm M ở ngoài ( O;R ) vẽ tiếp tuyến MC và cát tuyến MAB sao cho điểm O không nằm ngoài goc BMC. MO cắt (O) tại E,F (ME<MF)Giả sử (O;R) không đổi, điểm M cố định, cát tuyến MAB quay quanh M. Hãy tìm GTLN của tống MA+MB
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN MP) đến (O). Gọi K là trung điểm của NPa, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ haib, Chứng minh tia KM là phân giác của góc
A
K
B
^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NPd, Gọi H là giao điểm của AB...
Đọc tiếp
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN < MP) đến (O). Gọi K là trung điểm của NP
a, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai
b, Chứng minh tia KM là phân giác của góc A K B ^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NP
d, Gọi H là giao điểm của AB và MO. Chứng minh: MA2 = MH.MO = MN.MP
e, Chứng minh bốn điểm N, H, O, P cùng thuộc một đường tròn
TỪ một điểm M nằm ngoài đường tròn kẻ tiếp tuyến MA MB nằm ngoài đường tròn . Lấy điểm E nằm ngoài đường trong sao cho AE>EB . Kẻ đường thẳng vuông góc với OE tại E cắt MA ơn C cắt MB kẻ Đ a, chứng mình C A E O thuộc dường tròn b, E là trung điểm của CD
Xem chi tiết
Cho (O) và điểm M nằm ngoài đường tròn (O). Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O)(A,B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D. a)Chứng minh tứ giác MAOB nội tiếp b)Gọi H là giao điểm của MO và AB. Chứng minh: MC.MDMA^2. Từ đó suy ra MC.MDMH.MO c)Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O)
Đọc tiếp
Cho (O) và điểm M nằm ngoài đường tròn (O). Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O)(A,B là các tiếp điểm). Qua M kẻ cát tuyến MCD với đường tròn (O) sao cho điểm C nằm giữa hai điểm M và D. a)Chứng minh tứ giác MAOB nội tiếp b)Gọi H là giao điểm của MO và AB. Chứng minh: MC.MD=MA^2. Từ đó suy ra MC.MD=MH.MO c)Lấy K là trung điểm của CD. Gọi E là giao điểm của BA và OK. Chứng minh EC là tiếp tuyến của (O)
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{CAM}\) là góc tạo bởi dây cung CA và tiếp tuyến AM
Do đó: \(\widehat{ADC}=\widehat{CAM}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{MDA}=\widehat{MAC}\)
Xét ΔMDA và ΔMAC có
\(\widehat{MDA}=\widehat{MAC}\)(cmt)
\(\widehat{AMD}\) là góc chung
Do đó: ΔMDA∼ΔMAC(g-g)
⇔\(\dfrac{MD}{MA}=\dfrac{MA}{MC}\)(Các cặp cạnh tương ứng tỉ lệ)
⇔\(MA^2=MC\cdot MD\)(đpcm)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(MA^2=MH\cdot MO\)(2)
Từ (1) và (2) suy ra \(MH\cdot MO=MC\cdot MD\)(đpcm)
Đúng 3
Bình luận (0)
c) để chứng minh EC là tiếp tuyến:
chứng minh tứ giác OECH nội tiếp thì ta sẽ có góc OHE=OCE=90o(đpcm)
=> cần chứng minh tứ giác OECH nội tiếp:
ta có: DOC=DHC (ccc CD)
xét MHC=MDO (tam giác MCH~MOD)= OCD (vì DO=OC)=OHD (cùng chắn OD) => HA là phân giác CHD
DOC=DHC => 1/2 DOC= 1/2 DHC =COE=CHE
mà COE với CHE cùng chắn cung CE trong tứ giác OHCE nên tứ giác đấy nội tiếp => xong :))))
Đúng 1
Bình luận (0)
Cho đường tròn left(Oright) và điểm M nằm ngoài đường tròn. Từ M, vẽ các tiếp tuyến MA,MB (A,B là các tiếp điểm). Lấy I nằm trong cung nhỏ AB (I khác A,B). Từ I, vẽ tiếp tuyến thứ ba của đường tròn left(Oright), tiếp tuyến đó cắt MA,MB tại E,F. Cho hat{AOB}120^o, tìm giá trị nhỏ nhất của S_{OEF}.
Đọc tiếp
Cho đường tròn \(\left(O\right)\) và điểm \(M\) nằm ngoài đường tròn. Từ \(M\), vẽ các tiếp tuyến \(MA,MB\) (\(A,B\) là các tiếp điểm). Lấy \(I\) nằm trong cung nhỏ \(AB\) (\(I\) khác \(A,B\)). Từ \(I\), vẽ tiếp tuyến thứ ba của đường tròn \(\left(O\right)\), tiếp tuyến đó cắt \(MA,MB\) tại \(E,F\). Cho \(\hat{AOB}=120^o\), tìm giá trị nhỏ nhất của \(S_{OEF}\).
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.b) Chứng minh: CH* OH.HM.
Đọc tiếp
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,
MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.
a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.
b) Chứng minh: CH* = OH.HM.
a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot HM=HB^2\)
=>\(OH\cdot HM=HB\cdot HC\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; 9cm). Từ điểm M nằm ngoài (O) về tiếp tuyến MA với đường tròn (A là tiếp điểm), biết MOA = 30°. Tính độ dài AM.
Xét ΔOAM vuông tại A có \(tanAOM=\dfrac{AM}{OA}\)
=>\(\dfrac{AM}{9}=tan30=\dfrac{1}{\sqrt{3}}\)
=>\(AM=\dfrac{9}{\sqrt{3}}=3\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)















