Lg

*Áp dụng định lý py-ta-go ta có: (Δ AHC)

AC²=AH²+HC²

20²=AH²+16²

400=AH²+256

AH²=144

AH=√144 =12

*Áp dụng định lý py-ta-go ta có: (Δ AHB)

AB²=AH²+BH²

AB²=12²+9²

AB²=225

AB=√225 =15

\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)

\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)

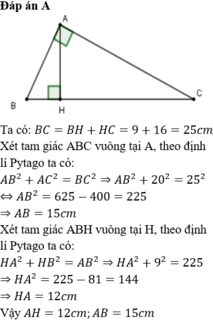
\(BC=BH+HC=9+16=25\left(cm\right)\)

Áp dụng định lý pitago vào tam giác vuông ABC, có:

\(BC^2=AB^2+AC^2\)

\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)

Áp dụng định lý pitago vào tam giác vuông ABH, có:

\(AB^2=BH^2+AH^2\)

\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)

Ta có :

BC = BH + HC

=> BC = 9 + 16

=> BC = 25 (cm)

Xét Δ ABC vuông tại A, có :

\(BC^2=AB^2+BC^2\) (định lí Py - ta - go)

=> \(25^2=AB^2+20^2\)

=> \(AB^2=225\)

=> AB = 15 (cm)

Xét Δ ABH vuông tại H, có :

\(AB^2=BH^2+AH^2\) (định lí Py - ta - go)

=> \(15^2=9^2+AH^2\)

=> \(AH^2=144\)

=> AH = 12 (cm)

Áp dụng pytago thôi,dễ mà

bạn dùng định lý pitago  thì biết ngay mà

bạn lên google 
tìm hệ thức lượng trong tam giác là có CT giải bài này cực nhanh luôn!

                      

*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ACH, ta có :

\(\Rightarrow\)AC² = HC² + AH²

\(\Rightarrow\)20²  = 16² + AH²

\(\Rightarrow\)AH² = 400 - 256

\(\Rightarrow\)AH² = 144

\(\Rightarrow\)AH = 12 (cm)

*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ABH, ta có :

\(\Rightarrow\)AB² = AH² + HB²

\(\Rightarrow\)AB² = 12² + 9²

\(\Rightarrow\)AB² = 225

\(\Rightarrow\)AB   = 15 (cm)

Vậy AB = 15 cm; AH = 12 cm

cảm ơn bạn rất nhiều!

△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow BC=\sqrt{15^2+20^2}=25\left(cm\right)\)

\(\Rightarrow CH=BC-BH=25-9=16\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=15^2+20^2=625\)

hay BC=25(cm)

Ta có: BH+CH=BC(H nằm giữa B và C)

nên CH=BC-BH=25-9=16(cm)

Vậy: CH=16cm

Bài 3 :

\(BC=HC+HB=16+9=25\left(cm\right)\)

\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)

\(\Rightarrow AB=15\left(cm\right)\)

\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)

Bài 6:

\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)

\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC) 

\(BC=BH+HC=2+2=4\left(cm\right)\)

Chu vi Δ ABC :

\(4+4+4=12\left(cm\right)\)

Xét △BHC vuông tại H có: BH² + HC²​ = BC²​ (định lý Pytago)

=> BH²​ + 16²​ = 20²​ 

=> BH²​ = 20²​ - 16²​ = 400 - 256 = 144

=> BH = 12 (cm)

Xét  △BHA vuông tại H có: BH² + AH² = AB² (định lý Pytago)

=> 12² + 9² = AB² 

=> AB² = 144 + 81 = 225

=> AB = 15 (cm)

Ta có: AC = AH + HC = 9 + 16 = 25

Xét △ABC có: 

AC² = 25² = 625

AB² + BC² = 15² + 20² = 225 + 400 = 625

=> AC² = AB² + AC² 

=> △ABC vuông tại A

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
   AB² = AH² +  HB² (định lý Py-ta-go)
   20²  = AH² + 16²
   400  = AH² + 256
   AH² = 400 - 256
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   AC² = 12²  + 5²
   AC² = 144  + 25
   AC² = 169
   AC  = \(\sqrt{169}\)= 13 (cm)

Vậy AH = 12 cm
       AC = 13 cm

Bài 2:
Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   15²  = AH² + 9²
   225  = AH² + 81
   AH² = 225 - 81
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHB vuông tại, ta có:
   AB² = AH² + HB² (định lý Py-ta-go)
   AB² = 12²  + 5²
   AB² = 144  + 25
   AB² = 169
   AB  = \(\sqrt{169}\)= 13 (cm)

Vậy AB = 13 cm

Câu này dễ

AH 12cm

AC13cm

AB13cm

87676ujgfszer546l5uy

Vẽ hình ra thì nó " siêu to khổng lồ " lắm :)

Ta có : BC = BH + HC = 9 + 16 = 25cm

Áp dụng định lí Pytago cho tam giác vuông ABC có :

BC² = AB² + AC² 

AB = \(\sqrt{25^2-20^2}=15cm\)

Áp dụng định lí Pytago cho tam giác vuông ABH có :

AB² = BH² + AH²

AH = \(\sqrt{15^2-9^2}=12cm\)

Vậy AB = 15cm , AH = 12cm

Hình tự vẽ :)

Ta có : BC = BH + HC = 9 + 16 = 25 (cm)

Tam giác ABC vuông tại A nên :

BC2 = AB2 + AC2

252 = AB2 + 162

=> AB2 = 252 - 202

AB2 = 625 - 400 = 225 = 152

=> AB = 15 (cm)

Tam giác AHC vuông tại H nên :

AC2 = AH2 + HC2

202 = AH2 + 162

=> AH2 = 202 - 162

AH = 400 - 256 = 144 = 122

=> AH = 12 (cm)

Vậy AB = 15 cm ; AH = 12 cm

Áp dụng định lí Pytago vào tam giác ABC ta có:

B C 2 = A B 2 + A C 2 suy ra: A B 2 = B C 2 - A C 2 = 20 2 - 12 2 = 256

Nên AB = 16cm

* Xét tam giác AHB và tam giác CAB có:

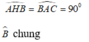
Suy ra: Δ AHB và CAB đồng dạng ( g.g) .

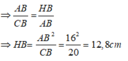
Chọn đáp án D