a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có

góc C chung

Do đó: ΔCDA\(\sim\)ΔCEB

b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có 

\(\widehat{AHE}=\widehat{BHD}\)

Do đó: ΔHEA\(\sim\)ΔHDB

Suy ra: HE/HD=HA/HB

hay \(HE\cdot HB=HD\cdot HA\)

a)

Xét (O) có

M là trung điểm của dây BC(gt)

nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)

Xét tứ giác BMOF có 

\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)

nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.

- Từ giả thiết suy ra: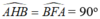 

=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)

Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB

- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC

Khi đó: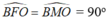 

Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).

Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB

* Chứng minh HE // BD.

Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.

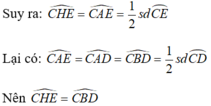
Và chúng ở vị trí so le trong suy ra: HE // BD

1: góc ADC=góc AFC=90 độ

=>ADFC nội tiếp

+ ) Ta thấy ngay hai tam giác vuông AHC và ANC có chung cạnh huyền AC nên A, H, N, C cùng thuộc đường tròn đường kính AC.

\(\Rightarrow\widehat{HNA}=\widehat{HCA}\) (Hai góc nội tiếp cùng chắn cung AH)

Ta thấy ngay hai tam giác vuông AMB và AHB có chung cạnh huyền AB nên A, M, H, B cùng thuộc đường tròn đường kính AB.

\(\Rightarrow\widehat{HMN}=\widehat{ABH}\) (Góc ngoài tại đỉnh đối diện bằng góc trong tại đỉnh)

Vậy nên \(\Delta ABC\sim\Delta HMN\left(g-g\right)\)

+) Ta có \(\widehat{ADC}=\widehat{ABC}\)  (Hai góc nội tiếp cùng chắn cung AC)

Mà \(\Delta ABC\sim\Delta HMN\Rightarrow\widehat{ABC}=\widehat{HMN}\) 

nên \(\widehat{ADC}=\widehat{HMN}\)

Chúng lại ở vị trí so le trong nên DC // HM

Ta có \(DC\perp AC\Rightarrow HM\perp AC\)

Gọi J là trung điểm AB

Ta có ngay IJ là đường trung bình tam giác ABC nên IJ // AC

Vậy nên \(HM\perp IJ\)

Mà J là tâm đường tròn ngoại tiếp tứ giác AMHB nên IJ vuông góc cung HM tại trung điểm HM hay IJ là trung trực của HM.

Vậy thì IM = IH.

Tương tự ta có IM = IH = IN hay I là tâm đường tròn ngoại tiếp tam giác HMN.

ad dqi

a: Xét ΔABE có

AD vừa là đường cao, vừa là trung tuyến

=>ΔABE cân tại A

b: Gọi M là giao của AD và FE

Xét ΔAME có

ED,AF là đường cao

ED cắt AF tại C

=>C là trực tâm

=>M,C,K thẳng hàng

=>ĐPCM