Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu.
Các câu hỏi tương tự
Cho nửa đường tròn tâm O, đường kính AB 2R, Ax và By là hai tiếp tuyến vởi nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh AM.BNR^2.
c) Tính tỉ số dfrac{S_{MON}}{S_{APB}} khi AMdfrac{R}{2}.
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến vởi nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh \(AM.BN=R^2.\)
c) Tính tỉ số \(\dfrac{S_{MON}}{S_{APB}}\) khi \(AM=\dfrac{R}{2}.\)
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Tam giác đếu ABC có độ dài cạnh là a, ngoại tiếp đường tròn.
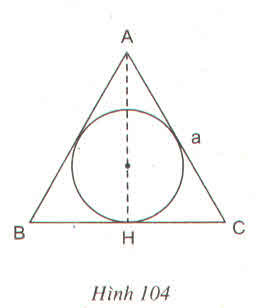
Cho hình quay một vòng xung quanh đường cao AH của tam giác đó (xem hình 104), ta được một hình nón ngoại tiếp một hình cầu. Tính thể tích phần hình nón bên ngoài hình cầu ?
a) Trong hình 102, cho A là giao điểm của đường tròn left(0;6right) với tia 90^0 và kí hiệu là Aleft(6;90^0right). Tương tự B là giao điểm của đường tròn left(0;3right) với tia 150^0 và kí hiệu là Bleft(3;150^0right). Hãy đánh dấu các điểm Cleft(6;210^0right),Dleft(3;30^0right),Eleft(6;330^0right) trên hình 102
b) Nối AB, BC, AD, DE và BD em thấy hình gì ?
Đọc tiếp
a) Trong hình 102, cho A là giao điểm của đường tròn \(\left(0;6\right)\) với tia \(90^0\) và kí hiệu là \(A\left(6;90^0\right)\). Tương tự B là giao điểm của đường tròn \(\left(0;3\right)\) với tia \(150^0\) và kí hiệu là \(B\left(3;150^0\right)\). Hãy đánh dấu các điểm \(C\left(6;210^0\right),D\left(3;30^0\right),E\left(6;330^0\right)\) trên hình 102
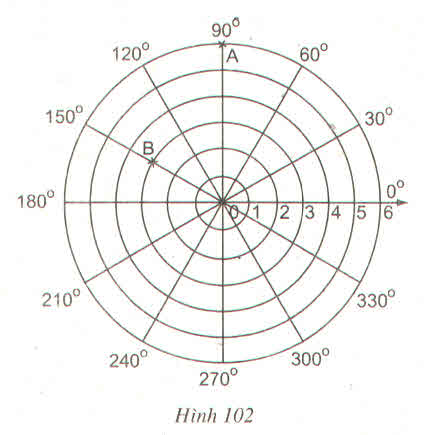
b) Nối AB, BC, AD, DE và BD em thấy hình gì ?
Trong các hình sau đây, hình nào có diện tích lớn nhất ?
(A) Hình tròn có bán kính 2cm
(B) Hình vuông có độ dài cạnh 3,5cm
(C) Tam giác với độ dài các cạnh là 3cm, 4cm, 5cm
(D) Nửa mặt cầu bán kính 4cm
chp (O;\(\frac{AB}{2}\)),M là trung điểm của OA.Qua M vẽ dây cung CD vuông góc với OA
a)chứng minh tứ giác ACOD là hình thoi
b)Tia CO cắt BD tại I.Chứng minh tứ giác DIOM nội tiếp
cho hình nón có bán kính r, đường sinh tạo với đáy một góc 60,tính thể tích của khối cầu nội tiếp khối nón
cho (O;6cm),từ 1 điểm A nằm ngoài (O) vẽ 2 tiếp tuyến AB,AC với (O).Tính khoảng cách từ tâm O đến dây BC,biết góc tạo bởi 2 cạnh AB và AC là 60o
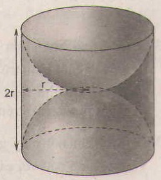
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị :cm). Người ta khoét rộng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).
một hình vuông có diện tích 50cm2.Tính thể tích hình cầu khi quay nửa đường tròn ngoại tiếp hình vuông đó




