Cho tam giác nhọn ABC , \(\widehat{A} = 75^0 , AB = 30\) mm ; BC = 35 mm . Hãy giải tam giác ABC ( làm tròn đến hàng đơn vị )

Những câu hỏi liên quan
a) cho tam giác ABC có \(\widehat{B}=40^0,\widehat{C}=30^0\). dựng điểm D khác phía với B sao cho \(\widehat{DAC}=\widehat{DCA}=50^0\)
Chứng minh rằng tam giác ABC cân.
b) chứng minh rằng chu vi một tam giác có các góc nhọn hơn 4 lần bán kính đường tròn ngoại tiếp tam giác.
câu a) mình nghĩ chứng minh ABD cân chứ ạ, sao lại ABC

Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.
Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)
Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 300
nên AK = \(\frac{1}{2}\)AC (2)
Từ (1) và (2) suy ra AK = AH
Xét \(\Delta\)AKB và \(\Delta\)AHD có:
^AKB = ^AHD (=900)
AK = AH(gt)
^BAK = ^DAH (=500)
Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)
=> AB = AD
Vậy \(\Delta\)ABD cân tại A(đpcm)
Cho tam giác nhọn ABC có đường cao AK. Kẻ KM vuông góc với AB tại M. Biết AK = 8cm, AB = 10cm, \(\widehat{ACB}=30^0\) Tính diện tích tứ giác BMNC
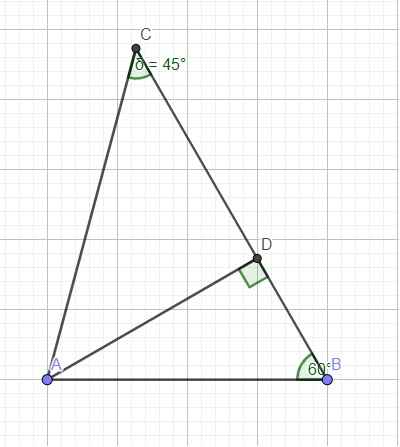
Cho tam giác ABC có góc A = 75 độ, AB = 10,6 cm, \(\widehat{B}\) : \(\widehat{C}\) = 4:3. Tính CA, CB và diện tích tam giác ABC
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có: \(\widehat{BAC}=15^0;\widehat{ABC}=30^0\). Gọi M là trung điểm AB. Tính \(\widehat{ACM}\)?
cho tam giác ABC góc A nhọn. Vẽ ra ngoài tam giác ABC các góc BAx và CAy sao cho \(\widehat{BAx}=\widehat{CAy}=30\) trên Ax lấy M, trên Ay lấy N sao cho AM=AB và AN=AC
a) CMR: BN=CM;
b) Gọi O là giao điểm của BN và CM tính \(\widehat{BOM}\)
Vẽ hình :
a) Xét \(\Delta ABN\) và \(\Delta AMC\) có :
\(AM=AB\left(GT\right)\)
\(AN=AC\left(GT\right)\)
\(\widehat{MAC}=\widehat{BAN}\left(=30^0+A\right)\)
Do đó : \(\Delta ABN=\Delta AMC\left(c-g-c\right)\)
Suy ra : \(BN=CM\) ( hai cạnh tương ứng )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác vuông ABC, \(\widehat{A}=90^0;\widehat{C}=30^0\) và đường phân giác BD (D thuộc cạnh AC)
a) Tính tỉ số \(\dfrac{AD}{CD}\)
b) Cho biết độ dài AB = 12,5cm. hãy tính chu vi và diện tích của tam giác ABC
a) Ta có ΔABC vuông tại A và \(\widehat{C}\) = 300
\(\Rightarrow\)AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm \(\Rightarrow\) BC = 25 cm Áp dụng định lí pitago vào tam giác ABC vuông tại A ta có : AC2= BC2 – AB2 = 252 – 12,52 AC = 21,65 (cm) CABC = AB+ BC+ CA =12,5+25+21,65 = 59,15(cm) SABC = 1/2AB.AC =1/2.12,5.21,65 = 135,31 (cm2)
\(\Rightarrow\)AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm \(\Rightarrow\) BC = 25 cm Áp dụng định lí pitago vào tam giác ABC vuông tại A ta có : AC2= BC2 – AB2 = 252 – 12,52 AC = 21,65 (cm) CABC = AB+ BC+ CA =12,5+25+21,65 = 59,15(cm) SABC = 1/2AB.AC =1/2.12,5.21,65 = 135,31 (cm2)
Đúng 0
Bình luận (1)
cho tam giác nhọn ABCcó 3 đường cao AD,BE,CF
a, chứng minh\(\Delta\) ABE\(\sim\)\(\Delta\) ACF
b, chứng minh tam giác AF*AC=AF*AB
c, chứng minh \(\widehat{AEF}=\widehat{ABC}\)
cho tam giác nhọn ABC có ABAC. Vẽ AE là tia phân giác của widehat{BAC}. trên AC lấy ADAB, kéo dài AB 1 đoạn BKDC. a)C/m: △AEB △AED và EA là tia phân giác củawidehat{BED} b)Kéo dài AB 1 đoạn BK DC, gọi H là giao điểm của AE và CK. C/m: AH ⊥ CK c)C/m: 3 điểm D,E,K thẳng hàng . Em cần gấp ạ.
Đọc tiếp
cho tam giác nhọn ABC có AB<AC. Vẽ AE là tia phân giác của \(\widehat{BAC}\). trên AC lấy AD=AB, kéo dài AB 1 đoạn BK=DC. a)C/m: △AEB = △AED và EA là tia phân giác của\(\widehat{BED}\) b)Kéo dài AB 1 đoạn BK = DC, gọi H là giao điểm của AE và CK. C/m: AH ⊥ CK c)C/m: 3 điểm D,E,K thẳng hàng . Em cần gấp ạ.
a: Xét ΔAEB và ΔAED có
AB=AD
góc BAE=góc DAE
AE chung
=>ΔAEB=ΔAED
=>góc BEA=góc DEA
=>EA là phân giác của góc BED
b: AK=AB+BK
AC=AD+DC
mà BK=DC; AB=AD
nên AK=AC
=>ΔAKC cân tại A
mà AH là phân giác
nên AH vuônggóc CK
c: Xét ΔEBK và ΔEDC có
EB=ED
góc EBK=góc EDC
BK=DC
=>ΔEBK=ΔEDC
=>góc KEB=góc CED
=>góc CED+góc CEK=180 độ
=>D,E,K thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat{B}=75^o57'19''\). Gọi \(M\) là trung điểm của \(AB\). Tính \(\widehat{ACM}?\) làm tròn đến giây.
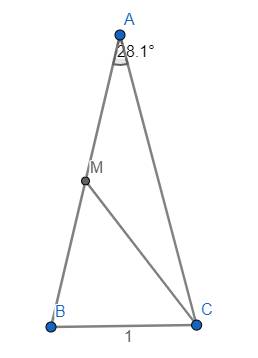
Không mất tổng quát, giả sử \(BC=1\).
Từ gt \(\Rightarrow\widehat{BAC}=180^o-2\widehat{ABC}=28^o5'22''\)
Áp dụng định lý sin cho tam giác ABC, ta có:
\(\dfrac{AC}{\sin B}=\dfrac{BC}{\sin A}\Rightarrow AC=\dfrac{BC\sin B}{\sin A}\) \(=\dfrac{\sin\left(75^o57'19''\right)}{\sin\left(28^o5'22''\right)}=2k\)
Mà tam giác ABC cân tại A nên \(AB=AC=2k\)
\(\Rightarrow MB=MA=k\)
Có \(MC=\sqrt{\dfrac{2\left(CA^2+CB^2\right)-AB^2}{4}}\) \(=\sqrt{\dfrac{2\left(4k^2+1\right)-4k^2}{4}}\) \(=\dfrac{\sqrt{4k^2+2}}{2}\) (Công thức tính độ dài đường trung tuyến trong tam giác, mình không chứng minh ở đây nhé.)
Áp dụng định lý sin cho tam giác ACM, có:
\(\dfrac{AM}{\sin\widehat{ACM}}=\dfrac{CM}{\sin\widehat{A}}\) \(\Rightarrow\sin\widehat{ACM}=\dfrac{AM\sin A}{CM}\) \(=\dfrac{k\sin\left(28^o5'22''\right)}{\dfrac{\sqrt{4k^2+2}}{2}}\)
\(\Rightarrow...\)
Đúng 2
Bình luận (0)