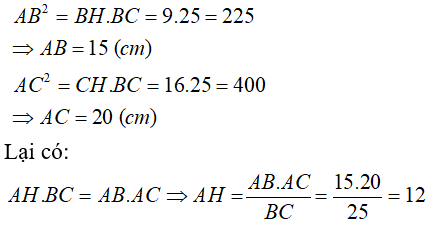Bài 3: Cho rABC vuông tại A (AB < AC) có đường cao AH và AH = 12 cm ; BC = 25 cm. a) Tìm độ dài của BH; CH; AB và AC. b) Vẽ trung tuyến AM. Tìm số đo của AM̂H. c) Tìm diện tích của rAHM.

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)
Bài 1:
AH=12cm
AC=20cm
\(\widehat{ABC}=37^0\)
Đúng 0
Bình luận (0)
Bài 5 : (3 điểm ) Cho tam giác ABC vuông tại A có AC = 12 cm và BC = 13 cm Đường cao AH b/Kẻ HD vuông góc với AB tại D , kẻ HE vuông góc với AC tại E . Chứng minh : HB.HC=DA.DB+EA.EC
b: \(DA\cdot DB+EA\cdot EC\)
\(=HD^2+HE^2\)
\(=AH^2=HB\cdot HC\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A (AB AC) có đường cao AH và AH 12 cm ; BC 25 cm.a) Tìm độ dài của BH; CH; AB và AC.b) Vẽ trung tuyến AM. Tính AMc) Tìm diện tích của rAHM.Bài 2: Cho tam giác DEF vuông tại D, đường cao DH. Biết DE 12 cm; EF 20. Tính DF; EH; FH.Bài 3: Cho tam giác DEF vuông tại D, đường cao DH. Biết EH 1 cm; FH 4 cm. Tính EF; DE; DF.Bài 4: BP 2017-2018Cho tam giác ABC vuông tại A, đường cao AH. Biết BH 4cm, CH 9cm.a) Tính độ dài đường cao AH và ABC của tam...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH và AH = 12 cm ; BC = 25 cm.
a) ![]() Tìm độ dài của BH; CH; AB và AC.
Tìm độ dài của BH; CH; AB và AC.
b) Vẽ trung tuyến AM. Tính AM
c) Tìm diện tích của rAHM.
Bài 2: Cho tam giác DEF vuông tại D, đường cao DH. Biết DE = 12 cm; EF = 20. Tính DF; EH; FH.
Bài 3: Cho tam giác DEF vuông tại D, đường cao DH. Biết EH = 1 cm; FH = 4 cm. Tính EF; DE; DF.
Bài 4: BP 2017-2018
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, CH = 9cm.
a) Tính độ dài đường cao AH và ABC của tam giác ABC.
b) Vẽ đường trung tuyến AM, (M e BC) của tam giác ABC. Tính AM và diện tích của tam giác
Bài 5. Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 3 và 4 . Hãy tính các cạnh góc vuông của tam giác vuông này, đường trung tuyến ứng với cạnh huyền và diện tích tam giác ABC
Bài 6. (1.0 điểm)
Cho tam giác ABC vuông tại A, có AB = 15cm và AC = 20cm. Tính độ dài đường cao AH và trung tuyến AM của tam giác ABC.
câu c bài 1 là tích diện tích của tam giác AHM nhá'
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác ABC vuông tại A có AH là đường cao, BH = 9 cm, CH = 16 cm. Tính BC, AH, AB, AC
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
bài 1 cho tam giác ABC vuông tại A, có AB 15 cm ;AC 20cm và đường cao AH. Tính độ dài đoạn thẳng BC và AHbài 2 cho tam giác ABC vuông tại AH,có AB 15cm,AH12cm.Tính BH,BC,CH,ACbài 3 cho tứ giác lồi ABCD có AC vuông góc vs BD tại O.Chứng minh AB2 + CD2 AD2+ BC2.giải giúp mình trong hôm nay với
Đọc tiếp
bài 1 cho tam giác ABC vuông tại A, có AB = 15 cm ;AC = 20cm và đường cao AH. Tính độ dài đoạn thẳng BC và AH
bài 2 cho tam giác ABC vuông tại AH,có AB =15cm,AH=12cm.Tính BH,BC,CH,AC
bài 3 cho tứ giác lồi ABCD có AC vuông góc vs BD tại O.Chứng minh AB2 + CD2 = AD2+ BC2.
giải giúp mình trong hôm nay với
bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
Đúng 0
Bình luận (0)
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm
Đúng 1
Bình luận (0)
Cho ∆ABC vuông tại A có 3 4 AB AC = và đường cao AH = 12 cm. Khi đó độ dài đoạn CH bằng
3 4 AB AC = là gì thế bạn? Bạn coi lại đề.
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có AB : AC = 3 : 4 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng CH bằng
đề là vậy phải ko
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH và AH= 12 cm , BC = 25cm . Tính AB , AC , BH , CH
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH.CH\Rightarrow x\left(25-x\right)=144\Leftrightarrow x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=9\\x=16\end{array}\right.\) (tm)
Nếu BH = 9 cm thì CH = 16 cm\(\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\left(cm\right)\)
Đúng 2
Bình luận (0)
Gỉa sử \(\Delta ABC\) có AB>AC
\(AB.AC=AH.BC=12.25=300\)
\(\Leftrightarrow2AB.AC=2.300=600\)
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2=25^2=625\) (1)
\(\left(1\right)\Rightarrow AB^2+AC^2-2AB.AC=625-600\)
\(\Leftrightarrow\left(AB-AC\right)^2=25\Leftrightarrow AB-AC=5\) (a) (Vì AB>AC \(\Rightarrow AB-AC>0\))
\(\left(1\right)\Rightarrow AB^2+AC^2+2AB.AC=600+625=1225\)
\(\Leftrightarrow\left(AB+AC\right)^2=1225\Rightarrow AB+AC=35\) (b)
Cộng vế vs vế của (a) và (b) ta được: \(2AB=40\Rightarrow AB=20\)
\(\Rightarrow AC=AB-5=20-5=15\)
Xét \(\Delta ABC\) vuông tại A, \(AH\perp BC\)\(\Rightarrow\) theo hệ thức lượng trong tam giác vuông ta có:
\(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{20^2}{25}=16\)
\(\Rightarrow CH=BC-BH=25-16=9\)
Đúng 2
Bình luận (1)
Sử dụng hệ thức lượng trong tam giác vuông thôi:
AB*AC = AH*BC = 12*25 = 300
AB^2 + AC^2 = BC^2 = 25^2 = 625
giải hệ trên ta được : AB = 15, AC = 20
AB^2 = BH*BC=> BH = AB^2/BC = 9
AH^2 = BH*CH=> CH = AH^2/BH = 12^2/9 = 16
NGOÀI RA HỆ PT TRÊN CÒN 1 NGHIỆM NỮA LÀ AB=20,AC=15
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 15: Cho AABC có AB = 5 cm; AC = 12 cm ; BC = 13 cm a) Chứng minh AABC vuông tại A và tính độ dài đường cao AH;b) Kẻ HEl AB tại E, HF perp AC tại F. Chứng minh: AE.AB=AF.AC c) Chứng minh: A AEF và AABC đồng dạng.