Để A(x) chia hết cho B(x) thì 

[(8x²-26x+a)-(2x-3)] chia hết cho 2x-3

=> [8x²-28x+a+3]chia hết cho 2x-3

ta có :

8x²-12x-16x+a+3=4x(2x-3)-16x+a+3

Để -16x+a+3 chia hết cho 2x-3 thì a+3=24 [để xuất hiện -8(2x-3)]

do đó a=21

V....

bạn tìm hiểu ở bài 12 sgk, đại khái ta sẽ có 

 x^4+6x^3+7x^2-6x+a chia  x^2+3x+1 dư a+3

mà để 2 đa thức chia hết thì x+3=0=)x=-3

thực ra còn có cách khác hay hơn, nhưng mình làm ko ra nên dùng tạm cách này, thông cảm :)

x^4+6x^3+7x^2-6x+a=x^4+2.3x.x^2+9x^2-6x-2x^2+a

=(x^2+3x)^2-2(3x+x^2)+a=(3x+x^2)(x^2+3x-2)+a

vậy a=3(3x+x^2)

tôi chịu, sai thì... T.T

\(\dfrac{A}{B}=\dfrac{8x^3+2x^2-8x-2-3}{4x+1}\)

\(=2x^2-2-\dfrac{3}{4x+1}\)

Vì \(f\left(x\right)⋮x-2;f\left(x\right):x^2-1\) dư 1\(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)=g\left(x\right)\cdot\left(x-2\right)\\f\left(x\right)=q\left(x\right)\left(x^2-1\right)+x=q\left(x\right)\left(x-1\right)\left(x+1\right)+x\end{matrix}\right.\) 

\(\Rightarrow\left\{{}\begin{matrix}f\left(2\right)=0\\f\left(1\right)=1\\f\left(-1\right)=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}32+4a+2b+c=0\\2+a+b+c=1\\2+a-b+c=-1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}4a+2b+c=-32\left(1\right)\\a+b+c=-1\left(2\right)\\a-b+c=-3\left(3\right)\end{matrix}\right.\)

 Trừ từng vế của (2) cho (3) ta được:

\(\Rightarrow2b=2\Rightarrow b=1\)

Thay b=1 vào lần lượt (1) ,(2),(3) ta được:

\(\Rightarrow\left\{{}\begin{matrix}4a+2+c=-32\\a+1+c=-1\\a-1+c=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\\a+c=-2\\a+c=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\left(4\right)\\a+c=-2\left(5\right)\end{matrix}\right.\)

Trừ từng vế của (4) cho (5) ta được:

\(\Rightarrow3a=-32\Rightarrow a=-\dfrac{32}{3}\Rightarrow c=-2+\dfrac{32}{3}=\dfrac{26}{3}\) Vậy...

Ta có

Vì phần dư R = 0 nên Phép chia đa thức (2 x 3 – 26x – 24) cho đa thức x 2 + 4x + 3 là phép chia hết.

Do đó (I) đúng.

Lại có

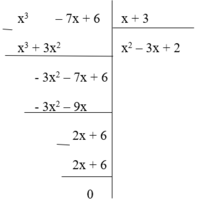
Nhận thấy phần dư R = 0 nên phép chia đa thức ( x 3 – 7x + 6) cho đa thức x + 3 là phép chia hết. Do đó (II) đúng

Đáp án cần chọn là: A

\(\Leftrightarrow2x^3-3x^2+x+a=\left(x+3\right)\cdot a\left(x\right)\)

Thay \(x=-3\Leftrightarrow-54-27-3+a=0\Leftrightarrow a=84\)