Cho hình thang ABCD đáy nhỏ là AB (AB//CD) có AB=3cm;AD=4cm;BD=6cm và DAB=DBC.Đường chéo AC cắt BD tại O.Qua B kẻ đg thẳng song song vs AD.Đường thẳng này cắt AC tại F và cắt CD tại E.
a)Chứng minh ∆ABD đồng dạng ∆BDC
b)Tính BC,CD
Cho hình thang cân ABCD. Biết đáy nhỏ AB = 3cm, cạnh bên BC = 2cm, đáy lớn CD = 5cm. Chu vi hình thang cân ABCD là:
Vì tứ giác ABCD là hình thang cân (gt).
=> AD = BC (Tính chất hình thang cân).
Mà BC = 2 (cm).
=> AD = 2 (cm).
Chu vi hình thang ABCD là:
AB + CD + BC + AD = 3 + 5 + 2 + 2 = 12 (cm).
p hình thang cân là :
3 + 5 + 2 + 2 = 12 cm
Đ/S : 12 cm
Hình thang ABCD có đáy nhỏ AB = 20 cm và đáy lớn CD= 25,4cm . Người ta kéo dài đáy AB về phía B 2cm và kéo dài đáy CD về phía C 3cm thì diện tích tăng thêm 37,5cm2 . Tính diện tích hình thang ABCD?
Chiều cao Hình thang ABCD :
37,5 x 2 : (2+3) = 15 (cm)
Diện tích hình thang là:
15 x (20+25,4) : 2 = 340,5 (cm2)
đ/s:.........
Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và D ^ = 45 ° . Độ dài đáy lớn CD bằng
A. 13cm.
B. 10cm.
C. 12cm.
D. 8cm.
Đáp án cần chọn là: A.
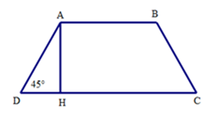
Ta có tam giác ADH vuông cân tại H vì D ^ = 45 ° .
Do đó DH = AH = 5cm
Mà DH = 1 2 (CD – AB)
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
Cho hình thang cân ABCD AB // CD đáy nhỏ AB =3cm đường cao AH=5 cm góc D=45 độ
Tính độ dài của đáy lớn CD
kẻ BK\(\perp\)DC
Xét ΔAHD vuông tại H có \(tanD=\dfrac{AH}{HD}\)
=>\(\dfrac{5}{HD}=tan45=1\)
=>HD=5/1=5(cm)
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAHD=ΔBKC
=>DH=KC
mà DH=5cm
nên KC=5cm
Ta có: AB//DC
\(H,K\in DC\)
Do đó: AB//HK
Ta có: AH\(\perp\)DC
BK\(\perp\)DC
Do đó: AH//BK
Xét tứ giác ABKH có
AB//KH
AH//BK
Do đó: ABKH là hình bình hành
=>AB=HK=3cm
DC=DH+HK+KC
=5+5+3
=13(cm)
Cho hình thang ABCD có đáy AB và CD, biết AB=4cm, CD=8cm, BC=5cm ,AD=3cm. CM : ABCD là hình thang vuông
GIÚP TỚ VỚI !!! MAI NỘP RỒI
Kẻ BH//AD(H∈CD)BH//AD(H∈CD), kẻ BD
Ta có:
+) AB//CD (hình thang ABCD)
⇒B2ˆ=D1ˆ⇒B2^=D1^ ( 2 góc so le trong )
+) BH//AD (cách vẽ)
⇒D2ˆ=B1ˆ⇒D2^=B1^ ( 2 góc so le trong)
Xét ΔDABΔDAB và ΔBHDΔBHD, ta có:
B2ˆ=D1ˆ(cmt)B2^=D1^(cmt)
BD : chung
D2ˆ=B1ˆ(cmt)D2^=B1^(cmt)
⇒⇒ ΔDABΔDAB = ΔBHDΔBHD (gcg)
⇒AD=BH⇒AD=BH
mà AD=3cm(gt)AD=3cm(gt)
⇒BH=3cm⇒BH=3cm
+) ΔDABΔDAB = ΔBHDΔBHD (cmt)
⇒AB=DH⇒AB=DH
mà AB=4cm(gt)AB=4cm(gt)
⇒DH=4cm⇒DH=4cm
+) DH+HC=DC(H∈DC)DH+HC=DC(H∈DC)
⇒4+HC=8⇒4+HC=8
⇒HC=4cm⇒HC=4cm
Xét ΔBHC,ΔBHC, ta có:
52=32+4252=32+42
⇒BC2=BH2+HC2⇒BC2=BH2+HC2 (Định lý Py-ta-go)
⇒ΔBHC⇒ΔBHC vuông tại H
⇒H1ˆ=900⇒H1^=900
+) AD//BH
⇒ADHˆ=H1ˆ⇒ADH^=H1^ (2 góc động vị)
⇒ADHˆ=900⇒ADH^=900
⇒⇒ Hình thang ABCD là hình thang vuông
Bạn ơi 900 là 90 độ nha
Cho hình thang cân ABCD AB // CD đáy nhỏ AB =3cm đường cao AH=5 cm góc D=45 độ
Tính độ dài của đáy lớn CD
Ạ=8cm
B=12cm
C=13cm
D=11cm
Cho hình thang cân ABCD có độ dài cạnh đáy là AB = 4cm, độ dài đáy CD gấp đôi độ dài đáy AB, độ dài chiều cao AH = 3cm. Tính diện tích hình thang cân.
Độ dài đáy CD là: 4 x 2 = 8 cm
Diện tích hình thang cân ABCD là: (4+8)x3:2 = 18 cm2
Độ dài đáy CD là: 4 x 2 = 8 cm Diện tích hình thang cân ABCD là: (4+8)x3:2 = 18 cm2
Bài 1. Hình thang ABCD có góc A= góc D= 90o, góc C= 40o. Đáy nhỏ AB= 4cm, đáy lớn CD= 8cm, AD= 3cm. Tính BC, góc ABC, diện tích hình thang ABCD.
Dựa vào hình thang ABCD (AB//CD) biết đáy lớn CD = 4cm, đáy nhỏ AB =3cm, cạnh bên AD =2cm và góc D=600
Cho hình thang cân abcd có đáy Ab=3cm đáy cd=5cm và cạnh bên aD=4cm tính chu vi hình thang cân abcd?
Chu vi hình thang cân là:
3+5+4+4=16(cm)
Đ/S:...
Vì ABCD là hình thang cân
=> AD = BC = 4cm
Chu vi hình thang cân ABCD là : 3+4+5+4=16 (cm)
Giải
Chu vi hình thang cân là :
3 + 5 + 4 + 4 = 16 ( cm )
Đáp số : 16 cm