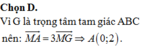Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có A (1;5), điểm B nằm trên đường thẳng (d1) : 2x + y + 1 = 0 và chân đường cao hạ đỉnh B xuống đường thẳng AC nằm trên đường thẳng (d2) : 2x + y − 8 = 0. Biết điểm M (3;0) là trung điểm của cạnh BC. Tìm tọa độ các đỉnh B và C của tam giác.
Những câu hỏi liên quan
15 tháng 2 2023 lúc 20:01
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)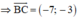 
Phương trình đường cao AH đi qua A(2;-1) nhận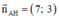 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có A(2;4); B(5;1); C(-1;-2) Phép tịnh tiến T B C → biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm của tam giác A’B’C’ là
A. (-4;2)
B. (4;2)
C. (4;-2)
D. (-4;-2)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm
G
(
2
3
;
0
)
, biết
M
(
1
;
1
)
là trung điểm cạnh BC. Tọa độ đỉnh A là: A. (2;0) B. (-2;0) C. (0;-2) D. (0;2)
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)
Trong không gian với hệ tọa độ
O
x
y
z
, cho tam giác ABC có đỉnh
C
-
2
;
2
;
2
và trọng tâm
G
-
1
;
2
;
2
.
Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt...
Đọc tiếp
Trong không gian với hệ tọa độ O x y z , cho tam giác ABC có đỉnh C - 2 ; 2 ; 2 và trọng tâm G - 1 ; 2 ; 2 . Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt phẳng (Oxy) và điểm B thuộc trục cao.
A. A(-1;-1;0), B(0;0;4)
B. A(-1;1;0), B(0;0;4)
C. A(-1;0;1), B(0;0;4)
D. A(-4;4;0), B(0;0;1)
trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;4), B(5;1), C(- 1; - 2). Phép tịnh tiến theo BC biến tam giác ABC tành tam giác A'B'C'. Tìm tọa độ trọng tâm của tam giác A'B'C'.Các bạn cho mình xin hình vẽ để dễ hình dung nhé.Mình cảm ơn !
\(\overrightarrow{BC}=\left(-6;-3\right)\)
Trọng tâm của ΔABC là G(2; 1)
Khi tịnh tiến ΔABC thành ΔA'B'C' theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thì G(2;1) cũng sẽ được tịnh tiến theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thành G' (x;y)
⇒ \(\overrightarrow{GG'}=\overrightarrow{BC}\) = (-6 ; -3)
⇒ \(\left\{{}\begin{matrix}x-2=-6\\y-1=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-2\end{matrix}\right.\). Vậy G' (-4 ; -2)
Đúng 0
Bình luận (0)
Câu 4.(2 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A 1;3 , B 2;1,C0;3 a). Tìm tọa độ trọng tâm tam giác ABC. b). Viết phương trình tổng quát đường trung trực của tam giác ABC. c). Tính khoảng cách từ A đến đường thẳng : x − y + 1 = 0
a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A(2;1);điểm B nằm trên trục hoành,điểm C nằm trên trục tung sao cho các điểm B,C có tọa độ không âm.Tìm tọa độ các điểm B;C sao cho tam giác ABC có diện tích lớn nhất.
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có các đỉnh A(-1;0); B(4;0);C(0;m).
Tìm tọa độ trọng tâm G của tam giác ABC theo m. Tìm m để tam giác GAB vuông tại G
Gọi \(\left(x_G;y_G\right)\) là tọa độ của G. Theo công thức tính trọng tâm tam giác, ta có :
\(\begin{cases}x_G=\frac{-1+4+0}{3}=1\\y_G=\frac{0+0+m}{3}=\frac{m}{3}\end{cases}\)
Vậy \(G\left(1;\frac{m}{3}\right)\)
\(\widehat{AGB}=90^0\Leftrightarrow\overrightarrow{BG}\perp AG\Leftrightarrow\overrightarrow{BG}.\overrightarrow{AG}=0\) (1)
\(\overrightarrow{BG}=\left(1-4;\frac{m}{3}-0\right)=\left(-3;\frac{m}{3}\right)\)
\(\overrightarrow{AG}=\left(1+1;\frac{m}{3}-0\right)=\left(2;\frac{m}{3}\right)\)
\(\overrightarrow{BG}.\overrightarrow{AG}=\frac{m^2}{9}-6\) (2)
Thay (2) vào (1) ta có : \(\widehat{AGB}=90^0\Leftrightarrow m^2=54\Leftrightarrow m=\pm3\sqrt{6}\)
Vậy có 2 giá trị cần tìm của m
Đúng 0
Bình luận (0)