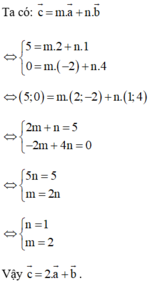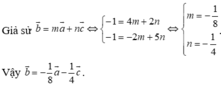Những câu hỏi liên quan
Cho 2 vectơ a, b thỏa mãn |vectơ a|=|vectơ b|=1,|4a-3b|=căn 13. Lập vectơ c=x. vectơ a +y. Vectơ b. Biết |c|=1 và vuông góc với vectơ a - b. Tính x, y
Xem chi tiết
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
Đúng 3
Bình luận (0)
1. Cho hình vuông ABCD cạnh a. Tính độ dài vectơ v= vectơ AC+ vectơ BD
2. Cho hình vuông tâm O cạnh a. Tính độ dài vectơ v= vectơ OA+ vectơ DC
Giúp mik giải nhanh
cho vectơ a =(-3;9) vectơ nào sau đây ko cùng phương với vecto a
A vectơ b =(-1;3)
B vectơ b (1;-3)
C vectơ b=(1;3)
D vectơ b =(-2;6)
Xem chi tiết
\( \dfrac{1}{3}\vec{a} = \dfrac{1}{3}(-3;9) = (-1;3)\)
Suy ra : A,B đúng
\( \dfrac{2}{3}\vec{a} = \dfrac{2}{3}(-3;9) = (-2;6)\)
Suy ra: D đúng
Chọn đáp án C
Đúng 3
Bình luận (0)
Cho vectơ a = (2; -2), vectơ b = (1; 4). Hãy phân tích vectơ c (5; 0) theo hai vectơ a và b.
Cho tam giác ABC, đặt vectơ a = vectơ AB, vectơ b = vectơ AC
a) Dựng các điểm M, N sao cho vectơ AM = 1/3AB, véctơ CN = 2BC
b) Phân tích các vectơ: CM, AN, MN qua các vectơ a, b
c) Gọi I là điểm thỏa mãn vectơ MI = vectơ CM. CMR I, A, N thẳng hàng
Xem chi tiết
a) Dựng các điểm M, N sao cho vectơ AM = 1/3AB, véctơ CN = 2BC
b) Phân tích các vectơ: CM, AN, MN qua các vectơ a, b
c) Gọi I là điểm thỏa mãn vectơ MI = vectơ CM. CMR I, A, N thẳng hàng
1. Cho tam giác ABC có trung tuyến AI.Đẳng thức vectơ nào sau đây đúng với mọi điểm O?
A. vectơ OA + vectơ OB + vectơ OC = 3 vectơ OI
B. 2 vectơ OA + vectơ OB + vectơ OC = vectơ 0
C. vectơ OA + vectơ OB + vectơ OC = vectơ 0
D. 2 vectơ OA + vectơ OB + vectơ OC = 4 vectơ OD
Cho các vectơ
a
→
4
;
-
2
;
b
→
-
1
;
-
1
;
c
→
2...
Đọc tiếp
Cho các vectơ a → = 4 ; - 2 ; b → = - 1 ; - 1 ; c → = 2 ; 5 . Phân tích vectơ b → theo hai vectơ a → và c → , ta được:
A. b → = - 1 8 a → - 1 4 c →
B. b → = 1 8 a → - 1 4 c →
C. b → = - 1 2 a → - 4 c →
D. b → = - 1 8 a → + 1 4 c →
Trong không gian Oxyz, cho vectơ
a
→
(1; -2; 3). Tìm tọa độ của vectơ
b
→
biết rằng vectơ
b
→
ngược hướng với vectơ
a
→
và |
b
→
| 2|
a
→
| A.
b
→
2...
Đọc tiếp
Trong không gian Oxyz, cho vectơ a → = (1; -2; 3). Tìm tọa độ của vectơ b → biết rằng vectơ b → ngược hướng với vectơ a → và | b → | = 2| a → |
A. b → = 2 ; - 4 ; 6 B. b → = 2 ; - 2 ; 3 C. b → = - 2 ; 4 ; - 6 b → = - 2 ; - 2 ; 3 D.
B. b → = 2 ; - 2 ; 3
C. b → = - 2 ; 4 ; - 6
D. b → = - 2 ; - 2 ; 3
Đáp án C
Vì vectơ b → ngược hướng với vectơ a → và | b → | = 2| a → | nên:
b → = -2 a → = (-2; 4; -6)
Đúng 0
Bình luận (0)