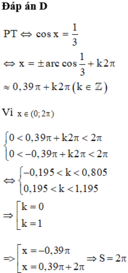Gọi S là tập hợp các nghiệm thuộc khoảng \(\left(0;100\pi\right)\) của phương trình \(\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2+\sqrt{3}cosx=3\) . Tổng các phần tử của S là

Những câu hỏi liên quan
Gọi S là tập hợp tất cả các nghiệm thuộc khoảng
0
;
100
π
của phương trình lượng giác
sin
π
2
+
cos
x
2
2
+
3
cos
x...
Đọc tiếp
Gọi S là tập hợp tất cả các nghiệm thuộc khoảng 0 ; 100 π của phương trình lượng giác sin π 2 + cos x 2 2 + 3 cos x = 3 . Tổng các phần tử của S là
A. 7400 π 3
B. 7525 π 3
C. 7375 π 3
D. 7550 π 3
Cho hàm số
y
f
x
liên tục trên
R
và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên
m
để phương trình
f
sin
x
3
sin
x
+...
Đọc tiếp
Cho hàm số y = f x liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π .Tổng các phần tử của S bằng
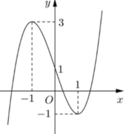
A. -5.
B. -8.
C. -6.
D. -10.
Chọn đáp án D.
![]()
khi đó yêu cầu bài toán trở thành phương trình
f t = 3 t + m
⇔ m = g t = f t - 3 t có nghiệm t ∈ ( 0 ; 1 ] . Có
![]()
Do đó
![]()
![]()
![]()
Vậy - 4 ≤ m < 1
![]()
Tổng các phần tử của tập S bằng -10.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f(sinx)3sinx+m có nghiệm thuộc khoảng
0
;
π
Tổng các phần tử của S bằng A. -5 B. -8 C. -6 D. -10
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f(sinx)=3sinx+m có nghiệm thuộc khoảng 0 ; π Tổng các phần tử của S bằng
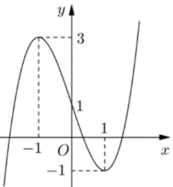
A. -5
B. -8
C. -6
D. -10
Đặt ![]() khi đó yêu cầu bài toán trở thành phương trình
khi đó yêu cầu bài toán trở thành phương trình
![]() có nghiệm
t
∈
(
0
;
1
]
Có
có nghiệm
t
∈
(
0
;
1
]
Có
![]()
Do đó
![]()
![]()
![]()
Vậy ![]()
Tổng các phần tử của tập S bằng -10.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
liên tục trên
ℝ
và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
f
sin
x
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng A. -10 B. -8 C. -...
Đọc tiếp
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng
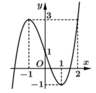
A. -10
B. -8
C. -6
D. -5
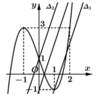
Đặt t = sinx do ![]()
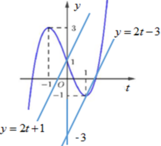
● Gọi ∆ 1 là đường thẳng qua điểm (1;-1) và song song với đường thẳng y = 3x nên có phương trình y = 3x - 4
● Gọi ∆ 2 là đường thẳng qua điểm (0;1) và song song với đường thẳng y = 3x nên có phương trình y = 3x+1
Do đó phương trình
f
sin
x
=
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
khi và chỉ khi phương trình f(t) = 3t + m có nghiệm thuộc nửa khoảng ![]() Chọn A.
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) 2sin x +m có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng: A. -10 B. -8 C. -6 D. -5
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
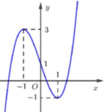
A. -10
B. -8
C. -6
D. -5
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình
2
sin
x
+
1
sin
x
+
2
m
có đúng hai nghiệm thuộc đoạn
0
;
π
. Khi đó S là A. một khoảng B. một đoạn C. một nửa khoảng D. một tập...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 = m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
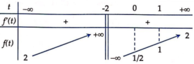
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng
Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình
2
sin
x
+
1
sin
x
+
2
m có đúng hai nghiệm thuộc đoạn
0
;
π
. Khi đó S là A. một khoảng B. một đoạn C. một nửa khoảng D. một tập hợp có hai phần t...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 =m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình
2
log
2
x
4
+
2
log
2
x
8
-
2
m
+
2018
0
có ít nhất một nghiệm thuộc đoạn
1
;
2
. Số phần tử...
Đọc tiếp
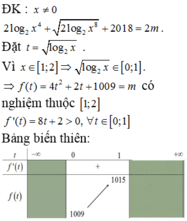
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình 2 log 2 x 4 + 2 log 2 x 8 - 2 m + 2018 = 0 có ít nhất một nghiệm thuộc đoạn 1 ; 2 . Số phần tử của S là
A. 7
B. 9
C. 8
D. 6
Gọi S là tổng các nghiệm thuộc khoảng
0
,
2
π
của phương trình 3.cos x – 1 0. Tính S.
Đọc tiếp
Gọi S là tổng các nghiệm thuộc khoảng 0 , 2 π của phương trình 3.cos x – 1 = 0. Tính S.
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc [−20; 20] để phương trình x 2 - 2 m x + 144 = 0 có nghiệm. Tổng của các phần tử trong SS bằng:
A. 21
B. 18
C. 1
D. 0
Phương trình có nghiệm khi ∆ = m 2 - 144 ≥ 0 ⇔ m 2 ≥ 12 2 ⇔ m ≥ 12 m ≤ − 12
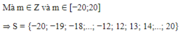
Do đó tổng các phần tử trong tập S bằng 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)