Đáp án A

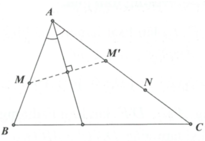
Phân tích.

- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.

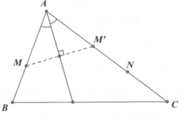
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.

- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.

- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.

Hướng dẫn giải.

Gọi M ' ∈   A C  là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.

Phương trình MM’ là:  3 x + y - 11 = 0

Toạ độ điểm I là nghiệm của hệ:

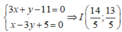
M’ đối xứng với M qua  

Đường thẳng AC qua N và M’ nên có phương trình:

Tọa độ A là nghiệm của hệ: 

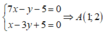
Đường thẳng AB đi qua A, M nên có phương trình:

x + y - 3 = 0

Gọi 

Do G là trọng tâm tam giác ABC nên ta có:

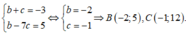
Vậy tọa độ các đỉnh của tam giác ABC là:

Chọn A

Phân tích.

     - Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.

     - Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.

     - Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.

     - Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.

Tọa độ trọng tâm là:

3x-5y=12 và 3x-7y=14

=>x=7/3 và y=-1

Gọi A(x1,y1); C(x2,y2)

Theo đề, ta có: x1+x2+1=7 và y1+y2-1=-3 và 3x1-5y1-12=0 và 3x2-7y2-14=0

=>x1+x2=6 và y1+y2=-2 và 3x1-5y1=12 và 3x2-7y2=14

=>x1=-1; x2=7; y1=-3; y2=1

=>A(-1;-3); C(7;1)

\(M=\left(m;8m+4\right)\) là trung điểm AC.

\(\Rightarrow A=\left(2m+5;16m+14\right)\)

Mà \(A\in AH\Rightarrow2m+5+2\left(16m+14\right)+1=0\)

\(\Rightarrow m=-1\)

\(\Rightarrow A=\left(3;-2\right)\)

Đường thẳng BC đi qua \(C=\left(-5;-6\right)\) và vuông góc AH có phương trình:

\(2x-y+4=0\)

B có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}8x-y+4=0\\2x-y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\Rightarrow B=\left(0;4\right)\)

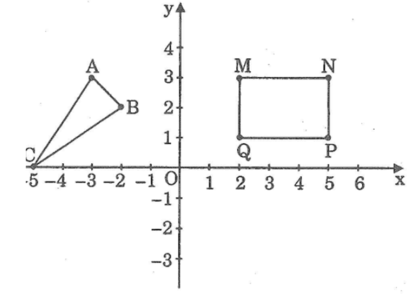
Toạ độ đỉnh của hình chữ nhật MNPQ là:

M(2;3); N(5;3);P(5;1);Q(2;1)

Toạ độ các đỉnh tam giác ABC là:

A(-3;3);B(-1;2);C(-5;0)

Đặt \(C\left(x;y\right)\)

Ta có: \(\left\{{}\begin{matrix}\overrightarrow{OM}=\left(2;4\right)\\\overrightarrow{CM}=\left(2-x;4-y\right)\end{matrix}\right.\)

Do O là trọng tâm tam giác và M là trung điểm AB \(\Rightarrow CM\) là trung tuyến

Theo tính chất trọng tâm:

\(\overrightarrow{CM}=3\overrightarrow{OM}\Rightarrow\left\{{}\begin{matrix}2-x=3.2\\4-y=3.4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-4\\y=-8\end{matrix}\right.\)

\(\Rightarrow C\left(-4;-8\right)\)

AH: x+y-1=0

=>VTPT là (1;1)

=>vecto BC=(1;1)

=>4-x=1 và 1-y=1

=>x=3 và y=0

=>B(3;0)

BK: 3x-y-7=0

=>VTPT là (3;-1)

=>vecto AC=(3;-1)

=>4-x=3 và 1-y=-1

=>x=1 và y=2

=>A(1;2)