Bài 1 :Giả sử đường thẳng (d) có phương trình y=ax+b . Xác định a,b để (d) đi qua hai điểm A(1;3) và B(-3;-1)
Bài 2 Cho hàm số y=x+m (d). Tìm các giá trị của m để đường thẳng (d)
1, Đi qua điểm A(1;2003)
2, Song song với đường thẳng x-y+3=0
Những câu hỏi liên quan
Bài 1 :Giả sử đường thẳng (d) có phương trình y=ax+b . Xác định a,b để (d) đi qua hai điểm A(1;3) và B(-3;-1)
Bài 2 Cho hàm số y=x+m (d). Tìm các giá trị của m để đường thẳng (d)
1, Đi qua điểm A(1;2003)
2, Song song với đường thẳng x-y+3=0
1. Cách viết phương trình đường thẳng đi qua 2 điểm1.1. Cách 1: Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)Gọi phương trình đường thẳng có dạng d: yax+bVì A và B thuộc phương trình đường thẳng d nên ta có hệThay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.1.2. Cách 2 giải nhanhTổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).Cách giải:Giả sử đường thẳng đ...
Đọc tiếp
1. Cách viết phương trình đường thẳng đi qua 2 điểm
1.1. Cách 1:
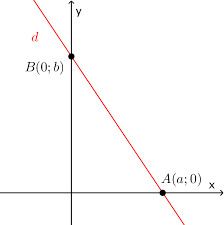
Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)
Gọi phương trình đường thẳng có dạng d: y=ax+bVì A và B thuộc phương trình đường thẳng d nên ta có hệ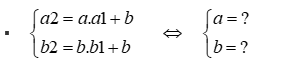
Thay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.1.2. Cách 2 giải nhanh
Tổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).
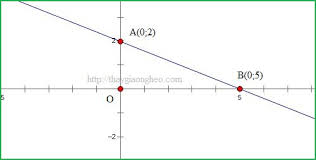
Cách giải:
Giả sử đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2) có dạng: y = ax + b (y*)
Vì (y*) đi qua điểm A(x1;y1) nên ta có: y1=ax1 + b (1)
Vì (y*) đi qua điểm B(x2;y2) nên ta có: y2=ax2 + b (2)
Từ (1) và (2) giải hệ ta tìm được a và b. Thay vào sẽ tìm được phương trình đường thẳng cần tìm.
Bài tập ví dụ viết phương trình đường thẳng đi qua 2 điểm
Bài tập 1: Viết phương trình đường thẳng đi qua hai điểm A (1;2) và B(0;1).
Bài giải:
Gọi phương trình đường thẳng là d: y=ax+by=ax+b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có:
⇔ 
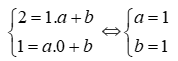
Thay a=1 và b=1 vào phương trình đường thẳng d thì d là: y=x+1
Vậy phương trình đường thẳng đi qua 2 điểm A và B là : y=x+1
Bài tập 2: Cho Parabol (P):y=–ײ . Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc (P) và có hoành độ lần lượt là 1 và 2.
Bài giải
Với bài toán này chúng ta chưa biết được tọa độ của A và B là như nào. Tuy nhiên bài toán lại cho A và B thuộc (P) và có hoành độ rồi. Chúng ta cần đi tìm tung độ của điểm A và B là xong.
Tìm tọa độ của A và B:
Vì A có hoành độ bằng -1 và thuộc (P) nên ta có tung độ y =−(1)²=–1 => A(1;−1)
Vì B có hoành độ bằng 2 và thuộc (P) nên ta có tung độ y =–(2)²=−4 ⇒ B(2;−4) còn cách khác k ?
Xác định phương trình của đường thẳng (d):y=ax+b biết đường thẳng (d) đi qua điểm A(-1;2) và điểm B(3; -2).
bài 1: cho hàm số y x^2 và y3x-2a) vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độb) Tìm hoành độ giao điểm của hai đồ thị đóbài 2: Cho (P) y-x^2/4 và (d): yx+ma) Vẽ (P)b) xác định m để (P) và (d) cắt nhau tại 2 điểm phân biệt A và Bc) xác định phương trình đường thẳng (d) song song với (d) và cắt (P) tại điểm có tung độ bằng -4bài 3: cho hàm số yax^2a) tìm a để (P) đi qua A(1;-1) vẽ (P) ứng với a vừa tìm đượcb) lấy điểm B trên (P) có hoành độ bằng -2.Viết phương trình đường thẳng ABbài...
Đọc tiếp
bài 1: cho hàm số y= x^2 và y=3x-2
a) vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) Tìm hoành độ giao điểm của hai đồ thị đó
bài 2: Cho (P) y=-x^2/4 và (d): y=x+m
a) Vẽ (P)
b) xác định m để (P) và (d) cắt nhau tại 2 điểm phân biệt A và B
c) xác định phương trình đường thẳng (d') song song với (d) và cắt (P) tại điểm có tung độ bằng -4
bài 3: cho hàm số y=ax^2
a) tìm a để (P) đi qua A(1;-1) vẽ (P) ứng với a vừa tìm được
b) lấy điểm B trên (P) có hoành độ bằng -2.Viết phương trình đường thẳng AB
bài 4: a) xác định hệ số a của hàm số y=ax^2 biết rằng đồ thị của hàm số đi qua điểm A (-2;1)
b) vẽ đồ thị của hàm số với a vừa tìm được
Bài 1: a) Cho hàm số f(x) (a- 1)x + b. Xác định hàm số biết f(-1) 2014 ; f(2) 2017b) Tìm m;n để đa thức P(x) mx3 + (m + 2)x2 - (3n - 5)x - 4n đồng thời chia hết cho x + 1 và x - 3Bài 2: Cho đường thẳng (d): y 4xviết phương trình đường thẳng (d1) song song với đường thẳng (d) và có tung độ gốc bằng 10Bài 3: Xác định a;b để đồ thị hàm số y ax + b đi qua A(3;-1) và B(-3;2)Bài 4: Cho 2 hàm số bậc nhất y x - m và y -2x + m - 1a) Xác định tọa độ giao điểm của đồ thị 2 hàm số khi m 2b) Vẽ đồ...
Đọc tiếp
Bài 1: a) Cho hàm số f(x) = (a- 1)x + b. Xác định hàm số biết f(-1) = 2014 ; f(2) = 2017
b) Tìm m;n để đa thức P(x) = mx3 + (m + 2)x2 - (3n - 5)x - 4n đồng thời chia hết cho x + 1 và x - 3
Bài 2: Cho đường thẳng (d): y = 4x
viết phương trình đường thẳng (d1) song song với đường thẳng (d) và có tung độ gốc bằng 10
Bài 3: Xác định a;b để đồ thị hàm số y = ax + b đi qua A(3;-1) và B(-3;2)
Bài 4: Cho 2 hàm số bậc nhất y = x - m và y = -2x + m - 1
a) Xác định tọa độ giao điểm của đồ thị 2 hàm số khi m = 2
b) Vẽ đồ thị 2 hàm số trên khi m = 2
c) Tìm m để đồ thị 2 hàm số cắt nhau tại 1 điểm trên trục tung
Bài 5: Viết phương trình đường thẳng (d) có hệ số góc bằng 7 và đi qua điểm M(2;-1)
Bài 6: Cho 3 đường thẳng: (d1): y = -2x + 3; (d2): y = 3x - 2; (d3): y = m(x + 1) - 5
a) Tìm m để 3 đường thẳng đã cho đồng quy
b) Chứng minh rằng đường thẳng (d3) luôn đi qua 1 điểm cố định khi m thay đổi
Bài 2: Cho (d): y = 2x + 3; (d’): y = - 3x - 2
a/ Xác định tọa độ giao điểm A của (d) và (d’)
b/ Viết phương trình đường thẳng đi qua A và có hoành độ luôn bằng tung độ
c/ Viết phương trình đường thẳng đi qua A và vuông với trục hoành
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ n...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4). a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút). c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Đúng 1
Bình luận (1)
đường thẳng (d) : y = ax +b đi qua hai điểm A (-1;-2 ) và B ( 3;-1
Từ pt đường thẳng d tìm được, hãy tìm phương trình đường thẳng d’ song song với d ?
Lời giải:
Vì $A, B\in (d)$ nên:
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -2=-a+b\\ -1=3a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{4}\\ b=\frac{-7}{4}\end{matrix}\right.\)
Vậy PTĐT $(d)$ là: $y=\frac{1}{4}x-\frac{7}{4}$
PTĐT $(d')$ song song với $(d)$ có dạng: $y=\frac{1}{4}x+m$ với $m\neq \frac{-7}{4}$
Đúng 1
Bình luận (0)