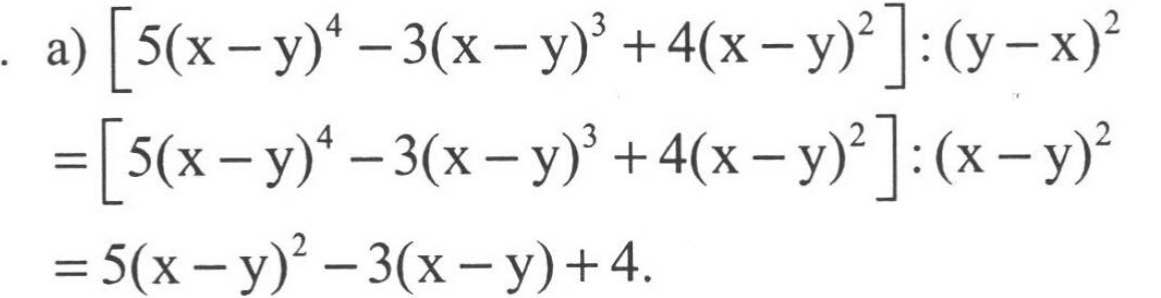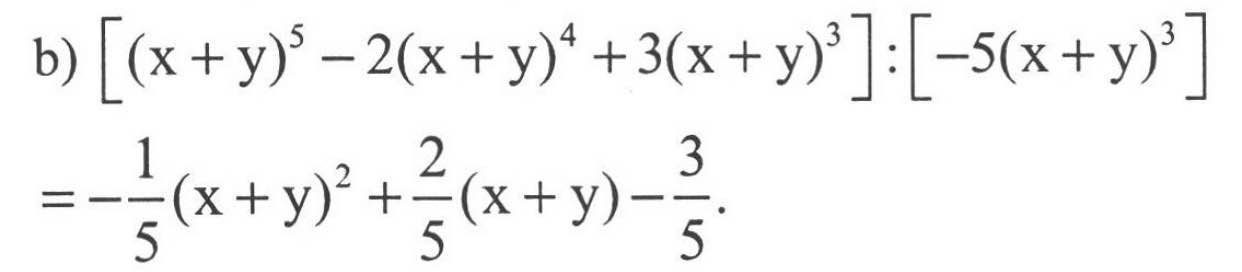X+y=5; x^2+y^2=17 . Tính x^5+y^5

Những câu hỏi liên quan
a, x/5 = y/2 và 3x - 2y = 44
b, x/3 = y/5 và x + y = -32
c, x/-2 = y/-3 và 4x - 3y = -32
d, x/5 = y/3 và x + y = 20
e, x/5 = y/3 và x - y = 20
g, x/5 = y/7 và x + y = 48
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\)
Do đó: x=-12; y=-20
Đúng 0
Bình luận (0)
Kết quả phân tích đa thức x^2(x - y)-(x - y) thành nhân tử là:
A. (x + 5) (x - y) B. (x - 5) (x - y) C. (x - 5) (x + y) D. (x + 5) (-x + y)
Phân tích đa thức \(x^2\) + 2xy + \(y^2\)- 25 thành nhân tử. Kết quả là:
A. (x + y - 5)(x – y + 5). B. (x + y - 5)(x + y + 5).
C. (x + y - 25)(x – y + 25). D. (x + y - 25)(x + y + 25).
Tìm x,y thuộc N,biết
1) (x+1) (y+2) = 5
2) (x+1) (y+2) = 6
3) (x+2) (y+3) = 6
4) (x -1) (y+3) = 6
5) (x -1) (y -3) = 5
6) (x -2) (y -1) = 3
7) (x -2) (y -1) = 5
8) (x -3) (y+1) = 7
Mẫu : 1) (x+1) (y+2) = 5 nên (x+1) và (y+2) Ư(5) = {1;5}
Trường hợp 1: x+1 = 1 thì y+2 = 5 nên x=0 và y=3 trường hợp 2: x+1 = 5 thì y+2 = 1 nên x=0 và y=
Lưu ý: ở cả hai trường hợp,1 và 5 là các ước của 5 Mn làm giống mẫu giúp mình với ạ
Xem chi tiết
tìm x,y,z biết:
câu 3:x/y=5/9 và x-y=-40
câu b: x/2=y/3 và 5.x-2.y=28
câu c: x/5=y/7=z/10 và x+y-z=20
câu d: x/3=y/4=z/5 và 3.x-2.y+2.z=121
câu e: x/4=y/2 và y/3=z/5 và x+y-z=20
3) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.9=90\end{matrix}\right.\)
4) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x}{10}=\dfrac{2y}{6}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=7.3=21\end{matrix}\right.\)
5) \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-z}{5+7-10}=\dfrac{20}{2}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.7=70\\z=10.10=100\end{matrix}\right.\)
6) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2y}{8}=\dfrac{2z}{10}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\Rightarrow\left\{{}\begin{matrix}x=11.3=33\\y=11.4=44\\z=11.5=55\end{matrix}\right.\)
7) \(\Rightarrow\dfrac{x}{12}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{12+6-10}=\dfrac{20}{8}=\dfrac{5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.12=30\\y=\dfrac{5}{2}.6=15\\z=\dfrac{5}{2}.10=25\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Câu 3:
\(\dfrac{x}{y}=\dfrac{5}{9}\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=5\\ \dfrac{y}{9}=10\Rightarrow y=90\)
Câu b:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\dfrac{x}{2}=7\Rightarrow x=14\\ \dfrac{y}{3}=7\Rightarrow y=21\)
Câu c:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-1}{5+7-10}=\dfrac{20}{2}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=50\\ \dfrac{y}{7}=10\Rightarrow y=70\\ \dfrac{z}{10}=10\Rightarrow z=100\)
Câu d:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\dfrac{x}{3}=11\Rightarrow x=3\\ \dfrac{y}{4}=11\Rightarrow y=44\\ \dfrac{z}{5}=11\Rightarrow z=55\)
Câu e:
\(\dfrac{x}{4}=\dfrac{y}{2}\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}\\\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10} \)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{8+6-10}=\dfrac{20}{4}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{6}=5\Rightarrow y=30\\ \dfrac{z}{10}=5\Rightarrow z=50\)
Đúng 1
Bình luận (0)
Bài 62 làm phép chia
a,[5.(x-y)^4-3.(x-y)^3+4.(x-y)^2]:(y-x)^2
b,[(x+y)^5-2.(x+y)^4+3.(x+y)^3]:[-5(x + y)^3]=0
Tìm x,y thuộc Z biết
a) x.y=5
b) (x+1). y=5
c) x.y+y-5=0
d) (x+y) . (y+1)=0
e) x.(y+1)+y.(y+1)=3
f)x.y+x+y^2+y-7=0
g) (x+2).(y-3)=5
cứu tui !!!!
phương trình nghiệm nguyên kiểu này liệt kê ước rồi kẻ bảng ra nhé
Đúng 1
Bình luận (0)
Tìm số nguyên x, y sao cho:
a) x. y = -5
b) x. y = -5 và x > y
c) (x + 1).(y - 2) = -5
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có: -5 = l.(-5)=(-5).l = (-l).5 = 5.(-l).
Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài.
a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1)
b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5).
c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1).
Đúng 0
Bình luận (0)
Tìm giá trị của x và y biết
1) x + y =10 và x= y. 2) 2.x + 3.y = 180 và x= y
3) x +y = 180 và x=y. 4) 3. x +5.y = 13 và y = 2.x
5) 3.x + 5.y = 13 và y = x + 1. 6) x+ y = 90 và x =2y
1) \(x+y=10\) mà \(x=y\) nên: \(x=y=\dfrac{10}{2}=5\)
2) \(2x+3y=180\) mà \(x=y\)
Ta có: \(2y+3y=180\Rightarrow5y=180\Rightarrow y=180:5=36\)
Vậy \(x=y=36\)
3) \(x+y=180\) mà \(x=y\) nên: \(x=y=\dfrac{180}{2}=90\)
4) \(3x+5y=13\) mà \(y=2x\) ta có:
\(3x+5\cdot2x=13\Rightarrow13x=13\Rightarrow x=1\)
\(y=2x=2\cdot1=2\)
Các câu còn lại bạn làm tương tự
Đúng 3
Bình luận (0)
a)Cho x+y=1 và xy=-6
Tính x^2+y^2;x^3+y^3;x^5+y^5
b)Cho x-y=1 và xy=6
Tính x^2+y^2; x^3-y^3; x^5-y^5
a. ta có : \(x^2+y^2=\left(x+y\right)^2-2xy=1^2-2\times\left(-6\right)=13\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=1^3-3\times\left(-6\right)\times1=19\)
\(x^5+y^5=\left(x+y\right)\left[x^4-x^3y+x^2y^2-xy^3+y^4\right]\)
\(=\left(x+y\right)\left[\left(x^2+y^2\right)^2-x^2y^2-xy\left(x^2+y^2\right)\right]=1.\left(13^2-\left(-6\right)^2-\left(-6\right).13\right)=211\)
b.\(x^2+y^2=\left(x-y\right)^2+2xy=1+2\times6=13\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=1^3+6.3.1=19\)
\(x^5-y^5=\left(x-y\right)\left[\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\right]\)
\(=\left(x-y\right)\left[\left(x^2+y^2\right)^2-x^2y^2+xy\left(x^2+y^2\right)\right]=1.\left(13^2-6^2+6.13\right)=211\)