1. Cho tam giác ABC đều. Trên tia đối của tia BC lấy E sao cho BA=BE; trên tia đối tia CB lấy D sao cho CD= CA. Tính góc EAD

Những câu hỏi liên quan
Cho tam giác ABC đều. Trên tia đối tia AB lấy D, trên tia đối tia BC lấy E, trên tia đối tia CA lấy F sao cho AD=BE=CF. CMR: tam giác DEF đều
cho tam giác đều ABC .Trên tia đối của tia AB lấy điểm D ,trên tia đối của tia BC lấy điểm E ,trên tia đối của tia CA lấy điểm F sao cho AD=BE=CF.Chứng minh tâm giác DÈ đều
cho tam giác ABC đều. Trên tia đối của tia AB lấy điểm D, trên tai đối của BC lấy điểm E, trên tia đối của tia CA lấy điểm F sao cho AD = BE = CF. Chứng minh tam giác DEF đều. Giúp mình với ạ
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) a) Chứng minh: Tam giác ABH= tam giác ACH b) Lấy điểm D trên tia đối của tia BC sao cho BD=BH, lấy E trên tia đối của tia BA sao cho BE=BA. Chứng minh: DE//AH
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) a) Chứng minh: Tam giác ABH= tam giác ACH b) Lấy điểm D trên tia đối của tia BC sao cho BD=BH, lấy E trên tia đối của tia BA sao cho BE=BA. Chứng minh: DE//AH Giải giúp mình với ◉‿◉
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔACH
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên BC lấy điểm E sao cho BA=BE. Tia phân giác của góc B cắt AC ở D. Trên BC lấy điểm E sao cho BA=BE
a) Chứng minh tam giác ABD= tam giác EBD
b) Chứng minh DE vuông góc với BC
c) Trên tia đối của tia AB lấy điểm M sao cho AM=EC, chứng minh MD=CD
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
c: Xét ΔDEC vuông tại E và ΔDAM vuông tại A có
DE=DA
EC=AM
Do đó: ΔDEC=ΔDAM
Suy ra: DC=DM
Đúng 2
Bình luận (1)
Cho tam giác ABC có AB = 2cm, BC = 4cm và \(\widehat{ABC}\) = 60o. Trên tia đối của tia BC lấy điểm D sao cho BD = BC, trên tia đối của tia BA lấy điểm E sao cho BE = BA. Tính diện tích tứ giác ACED.
mk cx đang bí câu này mà ko ai trả lời. chán thât!
Đúng 0
Bình luận (0)
giải giúp mình nha!
Cho tam giác ABC đều. Trên tia đối tia AB lấy điểm D, trên tia đối tia BC lấy điểm E, trên tia đối tia CA lấy điểm F sao cho AD=BE=CF. CMR:
Tam giác DEF đều
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = 1/3 BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.
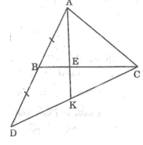
Trong ΔACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/3 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ΔACD.
Vì AK đi qua E nên AK là đường trung tuyến của ΔACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 2 cm; BC = 4 cm và ˆ A B C = 60 0 . Trên tia đối của tia BC lấy điểm D sao cho BD = BC, trên tia đối của tia BA lấy điểm E sao cho BE = BA. Tính diện tích tứ giác ACED.
+)Ta có:BA = BE (gt)
\(\implies\) B là trung điểm của AE\(\left(1\right)\)
+)Ta có:BD = BC (gt)
\(\implies\) B là trung điểm của DC\(\left(2\right)\)
Từ (1);(2) \(\implies\) B là trung điểm của AE ; DC
\(\implies\) AE và DC cắt nhau tại B
\(\implies\) Tứ giác ADEC là hình bình hành
+)Kẻ AH vuông góc với DC
Xét tam giác AHB có:
ABH + BAH + AHB =180 (tổng ba góc trong một tam giác)
\(\implies\) 60 + BAH + 90 =180
\(\implies\) BAH =30
\(\implies\) BH =\(\frac{1}{2}\) AB
\(\implies\) BH = \(1\) (cm)
Xét tam giác ABH vuông tại H có:
\(AH^2+BH^2=AB^2\) (định lý Py - ta - go)
\(\implies\) \(AH^2+1^2=2^2\)
\(\implies\) \(AH^2+1=4\)
\(\implies\) \(AH^2=3\) (cm)
Ta có: BH + HC = BC
\(\implies\)1 + HC = 4
\(\implies\) HC = 3 (cm)
Xét tam AHC vuông tại H có:
\(AH^2+HC^2=AC^2\) (định lý Py - ta - go)
\(\implies\) \(3+3^2=AC^2\)
\(\implies\) \(3+9=AC^2\)
\(\implies\) \(AC^2=12\)
\(\implies\) \(AC=\sqrt{12}\) (cm)
Ta có:HB + BD = HD
\(\implies\) 1 + 4 = HD
\(\implies\) HD = 5 (cm)
+)Xét tam giác AHD vuông tại H có:
\(AH^2+HD^2=AD^2\) (định lý Py - ta - go)
\(\implies\) \(3+5^2=AD^2\)
\(\implies\) \(3+25=AD^2\)
\(\implies\) \(28=AD^2\)
\(\implies\) \(AD=\sqrt{28}\) (cm)
Vậy diện tích hình tứ giác \(ACED\)\(=\sqrt{28}.\sqrt{12}=\sqrt{336}\) (cm)
Lần đầu tớ vẽ hình trên máy tính nên có gì sai sót thì cậu thông cảm cho

















