Cho tam giác ABC nhọn biết 3 góc của tam giác lập thành một cấp số cộng ; số đo góc A nhỏ nhất và sin A = 2 2 .Tìm các góc của tam giác?
A. 60º; 75º
B. 75º; 80º
C. 50º; 85º
D. 55º; 80º
Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25o. Tìm 2 góc còn lại?
A. 65o ; 90o
B. 75o ; 80o
C. 60o ; 95o
D. 60o ; 90o
Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25 độ. Tìm 2 góc còn lại?
A. 75 độ ; 80 độ.
B. 60 độ ; 95 độ.
C. 60 độ ; 90 độ.
D. 65 độ ; 90 độ.
Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25o. Tìm 2 góc còn lại?
A. 65o ; 90o
B. 75o ; 80o
C. 60o ; 95o
D. 55o; 100o
Chọn C
Gọi số đo ba góc ba góc lập thành cấp số cộng là 25; 25+ d ; 25 +2d có công sai d.
Tổng ba góc trong một tam giác bằng 1800 nên :
u 1 + u 2 + u 3 = 180 ⇔ 25 + 25 + d + 25 + 2 d = 180 ⇔ 3 d = 105 ⇔ d = 35 .
Vâỵ
u 2 = 25 + 35 = 60 ; u 3 = 25 + 2 . 35 = 95.
Ba cạnh một tam giác vuông có độ dài là các số nguyên dương lập thành một cấp số cộng có công sai bằng 2. Tìm ba cạnh đó
A. 3; 5; 7
B. 5; 7; 9
C. 4; 6; 8
D. 6; 8; 10
Ba góc của một tam giác vuông lập thành cấp số cộng. Số đo góc nhỏ nhất là
A. 40°
B. 15°
C. 30°
D. 45°
Ba góc của một tam giác vuông lập thành cấp số cộng. tìm số đo ba góc
Gọi 3 góc lần lượt là \(a;b;90\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=90\\2b=a+90\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=30\\b=60\end{matrix}\right.\)
Vậy số đo 3 góc là \(30^0;60^0;90^0\)
Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.
Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).
Độ dài các cạnh của một tam giác ABC lập thành một cấp số nhân. Tam giác ABC có tối đa mấy góc không vượt qua 60°?
A. 0
B. 1
C. 2
D. 3
Chọn C
Giả sử ba cạnh của tam giác ABC là a,b,c. u 1 + u 1 q 4 = 51
không mất tính tổng quát, ta giả sử 0 < a≤a≤b≤c, nếu chúng tạo thành cấp số nhân thì theo tính chất của cấp số nhân Ta có: b2=ac.
Theo định lý hàm côsin Ta có:
![]()
![]()
Mặt khác a 2 + c 2 ≥ 2 a c ⇒ cos B ≥ 1 − 1 2
Vậy góc B ^ ≤ 60 ° ,mà a ≤ b ⇒ A ≤ 60 ° , cho nên tam giác ABC có hai góc không quá 60°
Độ dài các cạnh của một tam giác ABC lập thành một cấp số nhân. Chứng minh rằng tam giác ABC có 2 góc không quá \(60^0\)
Giả sử 3 cạnh của tam giác ABC theo thứ tự a, b, c. Không giảm tính tổng quát, ta giả sử 0 < a \(\le b\le c\), nếu chúng tạo thành cấp số nhân thì, theo tính chất của cấp số nhân ta có : \(b^2=ac\)
Theo định lí hàm số côsin, ta có :
\(b^2=a^2+c^2-2ac\cos B\Rightarrow ac=a^2+c^2-2ac.\cos B\)
\(\Leftrightarrow\cos B=\frac{a^2+c^2}{2ac}-\frac{1}{2}\)
Mặt khác \(a^2+c^2\ge2ac\Rightarrow\cos B\ge1-\frac{1}{2}=\frac{1}{2}\)
Vậy góc \(B\le60^0\)
Nhưng \(a\le b\Rightarrow A\le60^0\) cho nên tam giác ABC có 2 góc không quá \(60^0\)
Cho tam giác ABC có các cạnh tương ứng a,b,c. Biết A =90° và a, ( 2 / 3 ) b , c theo thứ tự lập thành một cấp số nhân. Tìm số đo góc B.
A. 30°
B. 45°
C. 15°
D. 60°
Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
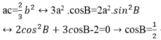
![]()