cho ΔABD vuông cân tại D và nội tiếp đtròn O. Dựng hình bình hành ABCD; gọi h là chân đường vuông góc kẻ từ D đến AC, K là giao điểm của AC với đtròn O. Cmr:
a/ tứ giác HBCD nội tiếp
b/ DOK=2.BDH
c/ CK.CA=2.BD2
Cho tam giác ADB vuông cân tại D (DA=DB) nội tiếp đường tròn tâm (O). Dựng hình bình hành ABCD. Gọi H là chân đường vuông góc kẻ từ D đến AC; K là giao điểm của AC với đường tròn (O). Chứng minh rằng:
a) Tứ giác HBCD nội tiếp
b) Góc DOK = 2* góc BDH
c) CK*CA=2*BD2
Cho đường tròn có 2 đường kinh AC và BD vuông góc với nhau . Dựng đường tròn (D,DC) cắt tia đối tia DC tại E.BE cắt AD và đường tròn (D) ở I và M.
a/ Cm BC là tiếp tuyến đtròn D và ABCD là hình vuông
b/ CM EM.EB =8R2
c/ Cm tứ giác IMCD nội tiếp . Xác định tâm O' và tính bán kính đtròn ngoại tiếp theo R.
GIÚP MIK VỚI ! MIK CẢM ƠN
Cho Tam giác ABD Vuông tại D . Nội tiếp đường tròn O dựng hình bình hành ABCD . Vẽ DH Vuông Góc AC , gọi K là giao điểm của AC với đường tròn O .
CM : Tứ giác HBCD nội tiếp
Góc DOK = 2 Góc BDH
CK.CA =2.BD2
cho tam giác ABC có A<90. Về phía ngoài tam giác ta dựng các tam giác vuông cân tại A là ΔABD,ACE.Dựng hình bình hành ADIE.
a)Chứng minh:BE=CD
b)Chứng minh:ΔABC=ΔDAI
c)Chứng minh: IA vuông góc với BC
Cho ABC nhọn (AB < AC) nội tiếp đtròn (O). Kẻ đường kính AK. Gọi H là giao điểm hai đường cao BE và AD của ABC.
a) Chứng minh: ABK, ACK là các vuông.
b) Chứng minh: CH AB tại F.
c) Chứng minh: Tứ giác BHCK là hình bình hành.
Cho tam giác ABC cân tại A nội tiếp (O). các tiếp tuyến của (O) vẽ từ A và C cắt nhau tại M. trên tia AM lấy điểm D sao cho AD=BC. CM:
a) ABCD hình bình hành.
b) AC, BD, OM đồng quy.
Hạ AH vuông góc BC
Tam giác ABC cân tại A => AH là đường trung trực bc => A , O , H thẳng hàng
Ta có AD vuông góc AO ( tia tiếp tuyến vuông góc bán kính đi qua tiếp điểm )
BC vuông góc AH
=> AD // BC
AD = BC => ADBC là hình bình hành
b, Gọi T là trung điểm của AC
ADBC là HBH => AC và BD giao nhau tại T
Theo tính chất 2 tiếp tuyến cắt nhau => AC vuông góc OM tại T
=> AC , BD, AC đồng quy tại T
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C.BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
2) CM cắt QN tại K, CN cắt PM tại L. Chứng minh rằng K L ⊥ O C .
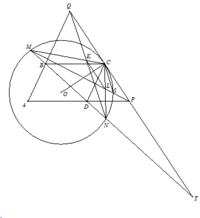
Gọi MP giao (O) tại điểm thứ hai S
Ta có các biến đổi góc sau:
K M L ^ = C M S ^ = S C P ^ (góc tạo bởi tiếp tuyến và dây cung)
= M S C ^ − S P C ^ (góc ngoài)
= M N C ^ − M N Q ^ (do các tứ giác MNPQ và MNSC nội tiếp).
= K N L ^
Từ đó tứ giác MKLN nội tiếp, suy ra K L M ^ = K N M ^ = Q P M ^ ⇒ K L ∥ P Q ⊥ O C
Vậy K L ⊥ O C .
cho tam giác ABC cân tại A nội tiếp đường tròn (O) .Vẽ hình bình hành ABCD tiếp tuyến tại C cắt đường thẳng AD tại M Cmr:
a) AD là tiếp tuyến của (O)
b) Ba đường thẳng AC, BD, OM đồng quy
a) Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Vì O là tâm (ABC) \(\Rightarrow OB=OC\Rightarrow OA\) là trung trực BC
\(\Rightarrow OA\bot BC\) mà \(BC\parallel AD\Rightarrow AD\bot OA\) \(\Rightarrow AD\) là tiếp tuyến
b) MO cắt AC tại E.
Vì MC,MA là tiếp tuyến \(\Rightarrow\Delta MAC\) cân tại M và MO là phân giác \(\angle AMC\)
\(\Rightarrow E\) là trung điểm AC
Vì ABCD là hình bình hành có E là trung điểm AC \(\Rightarrow B,E,D\) thẳng hàng
\(\Rightarrow AC,BD,OM\) đồng quy tại E
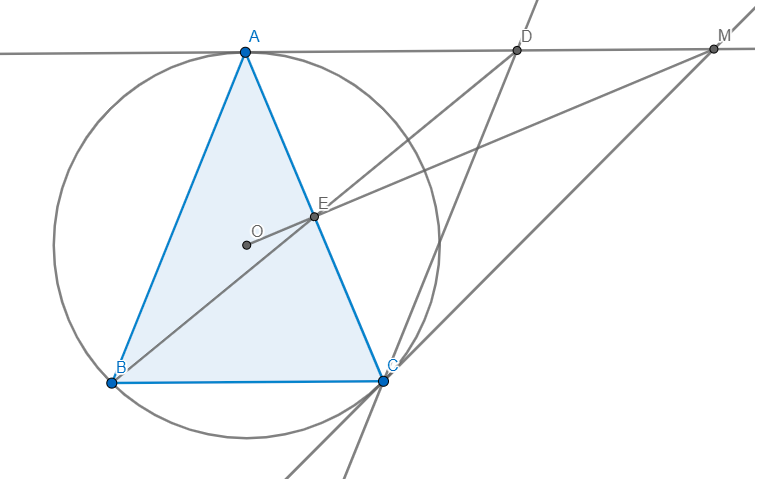
Cho tam giác ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh:
a, Đường thẳng AD là tiếp tuyến của (O)
b, Ba đường thẳng AC, BD và ON đồng quy
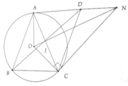
a, Tam giác ABC cân tại A nội tiếp (O)
=> OA ⊥ BC
=> OA ⊥ AD (vì AD//BC)
=> AD là tiếp tuyến của (O)
b, Chứng minh được ON là tia phân giác của A O D ^ mà ∆OAC cân tại O nên ON cũng là đường trung tuyến => ON cắt AC tại trung điểm I của AC => ON,AC,BD cùng đi qua trung điểm I của AC