Cho hình vẽ , biết Bx//Dy, góc B = 150 độ ; góc D= 120 độ .Tính BAD

Những câu hỏi liên quan
Cho hình vẽ biết Bx//Dy, góc B=45 độ , góc D = 30 độ. Tính góc BCD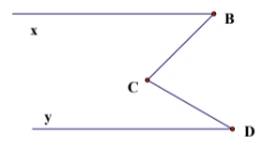
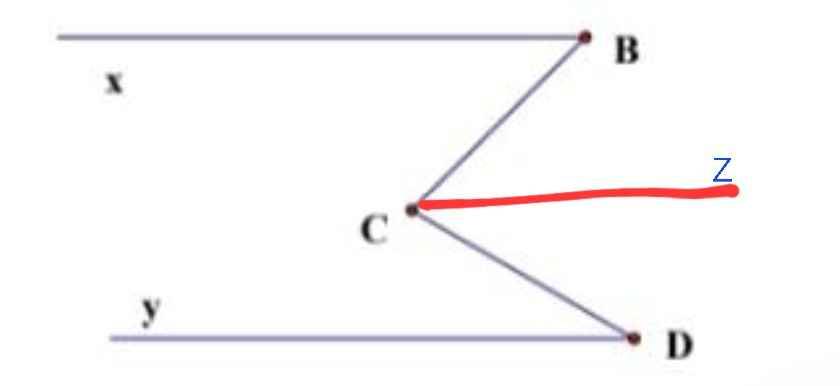
Vẽ tia Cz // Bx // Cy
Do Bx // Cz
⇒ ∠BCz = ∠xBC = 45⁰ (so le trong)
Do Cz // Dy
⇒ ∠DCz = ∠CDy = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCz + ∠DCz
= 45⁰ + 30⁰
= 75⁰
Đúng 2
Bình luận (0)
cho hình vẽ. Biết HK // BX; góc EX = 150 độ ; góc ABC = 80 độ. Câu a: tính số đo góc BAC. Câu b : tính số đo góc AKH.
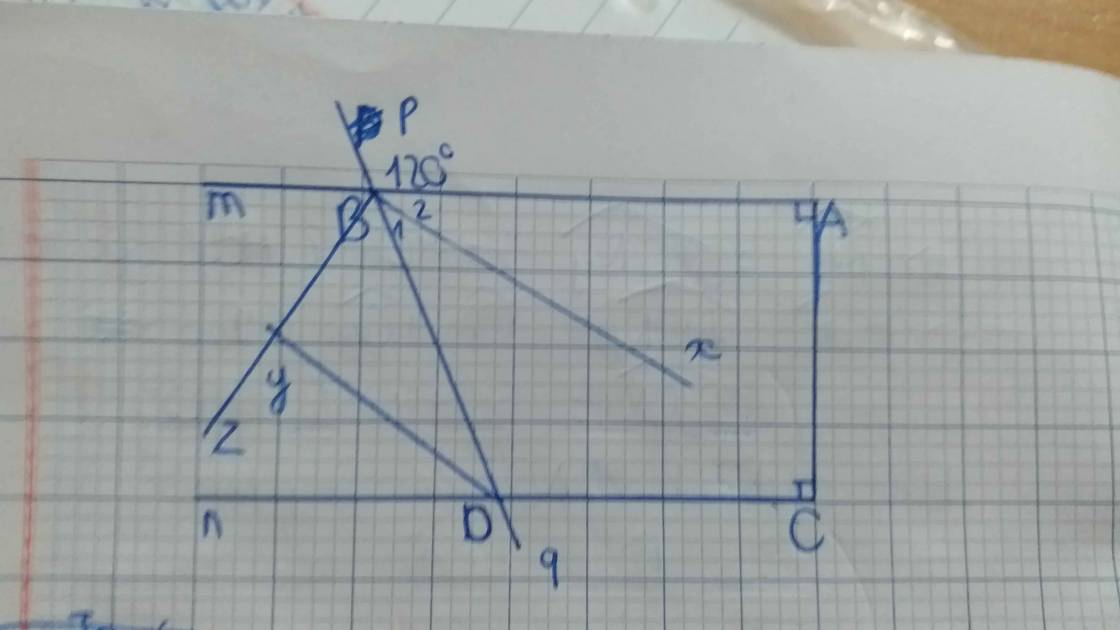 Cho hình vẽ: a) c/m AB//CD b) Tính các góc đỉnh B; D còn lại c) Bx là phân giác góc ABD Dy là phân giác góc BDn Bz là phân giác góc mBD Chứng minh Bx // Dy ; Bz vuông góc Dy
Cho hình vẽ: a) c/m AB//CD b) Tính các góc đỉnh B; D còn lại c) Bx là phân giác góc ABD Dy là phân giác góc BDn Bz là phân giác góc mBD Chứng minh Bx // Dy ; Bz vuông góc Dy
a: AB vuông góc AC
DC vuông góc AC
=>AB//DC
b: AB//CD
=>góc PBA=góc BDC
=>góc BDC=120 độ
góc BDn=180-120=60 độ
góc mBD=góc PBA=120 độ
góc mBP=góc ABD=180-120=60 độ
c: góc xBD=1/2*góc ABD=1/2*120=60 độ
góc yDB=1/2*góc BDn=1/2*120=60 độ
=>góc xBD=góc yDB
=>Bx//Dy
góc yBD+góc yDB
=1/2(góc mBD+góc nDB)
=1/2*180=90 độ
=>Bz vuông góc Dy
Đúng 0
Bình luận (0)
trên hình vẽ biết Bx song song Dy và B=101 độ D=74 đọ
Cho hình vẽ, biết Ax//Dy, góc xAd= 100 độ
a) Tính góc ADy
b) Biết góc ADE=110 độ, góc DEz=30 độ. Chứng minh Dy//Ez
c) Ax có song song với Ez không? vì sao
Cho Ax // Dy,số đo các góc trên hình vẽ,tính BCD biết góc B 120 độ,góc D 30 độ
Xem chi tiết
Cho hình vẽ biết Ex//Dy , góc E=120 độ ; góc G = 30 độ . Tính góc EDG 
Lời giải:
Kẻ $Dt\parallel Ex\parallel Gy$ ($Dt$ nằm cùng phía với $Ex$ trên mặt phẳng bờ $DE$)
Vì $Dt\parallel Ex$ nên:
$\widehat{xED}+\widehat{EDt}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{EDt}=180^0-\widehat{xED}=180^0-120^0=60^0$
Vì $Dt\parallel Gy$ nên $\widehat{tDG}=\widehat{DGy}=30^0$ (2 góc so le trong)
$\Rightarrow \widehat{EDG}=\widehat{EDt}+\widehat{tDG}=60^0+30^0=90^0$
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Vẽ tia Bx vuông góc AC; Dy vuông góc AC. Đường thẳng qua A vuông góc với BD cắt Bx tại N, cắt Dy tại M. Đường thẳng NQ cắt AD ở E, BC cắt ở F.
a) Cm: MNPQ, MEPF là hình bình hành
b) ABCD có đặc điểm gì để MNPQ là hình thoi?
Bài 1: Cho hình bình hành ABCD. Vẽ tia Bx vuông góc với AC, Dy vuông góc với AC. Đường thẳng qua A vuông góc với BD cắt Bx tại P, cắt Dy tại Q. Đường thẳng qua C vuông góc với BD cắt Bx tại N, cắt Dy tại M. Đường thẳng NQ cắt AD ở E, BC ở F. CMR: MNPQ, MEPF là hình bình hành.Bài 2: Cho tứ giác ABCD có AD BC, góc C và góc D tù. Gọi M, N, P, Q lần lượt là trung điểm AB, AC, CD, BD. MNPQ là hình gì? Chứng minh.
Đọc tiếp
Bài 1: Cho hình bình hành ABCD. Vẽ tia Bx vuông góc với AC, Dy vuông góc với AC. Đường thẳng qua A vuông góc với BD cắt Bx tại P, cắt Dy tại Q. Đường thẳng qua C vuông góc với BD cắt Bx tại N, cắt Dy tại M. Đường thẳng NQ cắt AD ở E, BC ở F. CMR: MNPQ, MEPF là hình bình hành.
Bài 2: Cho tứ giác ABCD có AD = BC, góc C và góc D tù. Gọi M, N, P, Q lần lượt là trung điểm AB, AC, CD, BD. MNPQ là hình gì? Chứng minh.













