Cho các số thực dương a, b ; a \(\ne\) b. Chứng minh:
\(\frac{\frac{\left(a-b\right)^3}{\left(\sqrt{a}-\sqrt{b}\right)^3}-b\sqrt{b}+2a\sqrt{a}}{a\sqrt{a}-b\sqrt{b}}+\frac{3a+3\sqrt{ab}}{b-a}=0\)
Những câu hỏi liên quan
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Đáp án D
Đặt log 25 x 2 = log 15 y = log 9 x + y 4 = t ⇒ x 2 = 25 t y = 15 t x + y = 4 . 9 t
⇒ 2 . 15 t + 15 t = 4 . 9 t x y = 2 5 3 t ⇒ 2 . 5 3 2 t + 5 3 t - 4 = 0 ⇔ [ 5 3 t = - 1 + 33 4 5 3 t = - 1 - 33 4
⇒ 5 3 t = - 1 + 33 4 ⇒ x y = - 1 + 33 4 ⇒ a = - 1 b = 33 ⇒ a + b = 32 .
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
−
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
19
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 19 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 34
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 , với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Cho a,b,c,d là các số thực dương
Đọc tiếp
Cho a,b,c,d là các số thực dương
Cho số thực x thỏa mãn
log
x
1
2
log
3
a
-
2
log
b
+
3
log
c
(a,b,c là các số thực dương). Hãy biểu diễn x theo a, b, c. A.
x
c
3
3
a
b...
Đọc tiếp
Cho số thực x thỏa mãn log x = 1 2 log 3 a - 2 log b + 3 log c (a,b,c là các số thực dương). Hãy biểu diễn x theo a, b, c.
A. x = c 3 3 a b 2
B. x = 3 a b 2 c 3
C. x = 3 a c b 2
D. x = 3 a c 3 b 2
Cho a,b,c là các số thực dương
Chứng minh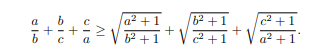 
19 tháng 12 2021 lúc 20:39
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
30 tháng 12 2020 lúc 21:24
Câu 1: Chứng minh frac{1}{1.2}+frac{1}{2.3}+frac{1}{3.4}+...+frac{1}{(n-1)n} với ∀n∈N^*Câu 2: Cho a,b,c là các số thực dương. Chứng minh rằng: frac{a^4+b^4+c^4}{a+b+c}geq abc.Câu 3: Cho các số thực dương a,b,c thỏa mãn ab+bc+ca3. Chứng minh rằng: sqrt{a^6+b^6+1}+sqrt{b^6+c^6+1}+sqrt{c^6+a^6+1}geq 3sqrt{3}Câu 4: Cho các số thực không âm a,b,c thỏa mãn a+b+c3.Chứng minh rằng: a^3+b^3+c^3geq 3Câu 5: Với a,b,c0 thỏa mãn điều kiện frac{a}{b}+frac{b}{c}+frac{c}{a}1. Chứng minh rằng: sqrtfrac{b}{a}+sqr...
Đọc tiếp
Câu 1: Chứng minh \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{(n-1)n}\) với ∀n∈\(N^*\)
Câu 2: Cho a,b,c là các số thực dương. Chứng minh rằng: \(\frac{a^4+b^4+c^4}{a+b+c}\geq abc\).
Câu 3: Cho các số thực dương a,b,c thỏa mãn \(ab+bc+ca=3\). Chứng minh rằng: \(\sqrt{a^6+b^6+1}+\sqrt{b^6+c^6+1}+\sqrt{c^6+a^6+1}\geq 3\sqrt{3}\)
Câu 4: Cho các số thực không âm a,b,c thỏa mãn \(a+b+c=3\).Chứng minh rằng: \(a^3+b^3+c^3\geq 3\)
Câu 5: Với \(a,b,c>0\) thỏa mãn điều kiện \(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\). Chứng minh rằng: \(\sqrt\frac{b}{a}+\sqrt\frac{c}{b}+\sqrt\frac{a}{c}\leq 1\)
1. Đề thiếu
2. BĐT cần chứng minh tương đương:
\(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Ta có:
\(a^4+b^4+c^4\ge\dfrac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{3}\left(ab+bc+ca\right)^2\ge\dfrac{1}{3}.3abc\left(a+b+c\right)\) (đpcm)
3.
Ta có:
\(\left(a^6+b^6+1\right)\left(1+1+1\right)\ge\left(a^3+b^3+1\right)^2\)
\(\Rightarrow VT\ge\dfrac{1}{\sqrt{3}}\left(a^3+b^3+1+b^3+c^3+1+c^3+a^3+1\right)\)
\(VT\ge\sqrt{3}+\dfrac{2}{\sqrt{3}}\left(a^3+b^3+c^3\right)\)
Lại có:
\(a^3+b^3+1\ge3ab\) ; \(b^3+c^3+1\ge3bc\) ; \(c^3+a^3+1\ge3ca\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow VT\ge\sqrt{3}+\dfrac{6}{\sqrt{3}}=3\sqrt{3}\)
Đúng 2
Bình luận (1)
4.
Ta có:
\(a^3+1+1\ge3a\) ; \(b^3+1+1\ge3b\) ; \(c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3\left(a+b+c\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
5.
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\) ; \(\dfrac{a}{b}+\dfrac{c}{a}\ge2\sqrt{\dfrac{c}{b}}\) ; \(\dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\)
\(\Rightarrow\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}+\sqrt{\dfrac{a}{c}}\le\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=1\)
Đúng 1
Bình luận (0)
Câu 1:
\(VT=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(VT=1-\dfrac{1}{n}< 1\) (đpcm)
Đúng 1
Bình luận (0)
Cho các thực dương a và số thực b khác 0. Mệnh đề nào sau đây là đúng? A.
log
2019
2019
a
3
b
2
1
+
1
3
log
2019
a
-
2
log
2019
b...
Đọc tiếp
Cho các thực dương a và số thực b khác 0. Mệnh đề nào sau đây là đúng?
A. log 2019 2019 a 3 b 2 = 1 + 1 3 log 2019 a - 2 log 2019 b
B. log 2019 2019 a 3 b 2 = 1 + 3 log 2019 a - 2 log 2019 b
C. log 2019 2019 a 3 b 2 = 1 + 1 3 log 2019 a - 2 log 2019 b
D. log 2019 2019 a 3 b 2 = 1 + 3 log 2019 a - 2 log 2019 b