\(\Delta ABC\) vuông tại A \(\Rightarrow\) \(AB^2+AC^2=BC^2\)(định lí Pytago)

\(\Delta DEF\)vuông tại D \(\Rightarrow\) \(DE^2+DF^2=EF^2\)(định lí Pytago)

Mà \(BC=EF,AC=DF\)\(\Rightarrow AB=DE\)

Xét \(\Delta ABC\) và \(\Delta DEF\) có:

\(AB=DE\left(cmt\right)\)

\(\widehat{A}=\widehat{D}=90^o\left(gt\right)\)

\(AC=DF\left(gt\right)\)

Vậy \(\Delta ABC=\Delta DEF\left(c.g.c\right)\)

ko biet vi chua hoc den lop 8

tôi chịu tôi chưa học lớp 8 nên tôi ko biết

bó tay . com .vn vì mình chưa học lớp 8 ^-^

a)

xét tam giác ABH vuông tại H có:

\(AH^2=AB^2-BH^2\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=12\)

theo tỉ lệ thức trong tam giác vuông ABC có:

\(AH^2=BH.CH\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=\frac{144}{5}=28,8\)

xét tam giác vuông AHC có:

\(AC^2=AH^2+HC^2\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{12^2+28,8^2}=\frac{156}{5}=31,2\)

vậy : \(\sin B=\frac{AH}{AB}=\frac{12}{13}\)

\(\sin C=\frac{AH}{AC}=\frac{12}{31,2}=\frac{5}{13}\)

b)

theo tỉ số lượng giác trong tam giác ABC có:

\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3.4}=2\sqrt{3}\)

xét tam giác vuông ABH có:

\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{3}\right)^2+3^2}=\sqrt{21}\)

theo hệ thức lượng trong tam giác vuông ABC có:

\(AC^2=BC.HC\Rightarrow AC=\sqrt{BC.HC}=\sqrt{7.4}=2\sqrt{7}\)

Vậy : \(\sin B=\frac{AH}{AB}=\frac{2\sqrt{3}}{\sqrt{21}}=\frac{2\sqrt{7}}{7}\)

\(\sin C=\frac{AH}{AC}=\frac{2\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{7}\)

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.

b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.

c)

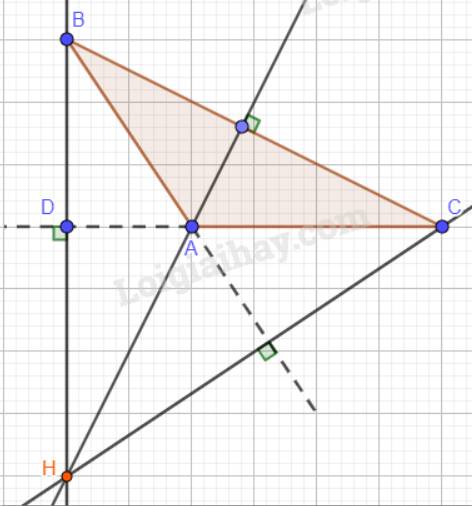
Nhận xét: H nằm ngoài tam giác ABC.

a: \(\widehat{B}=90^0-30^0=60^0\)

XétΔABC vuông tại A có 

\(\sin C=\dfrac{AB}{BC}\)

nên AB=5cm

=>\(AC=5\sqrt{3}\left(cm\right)\)

b: \(\widehat{C}=90^0-30^0=60^0\)

Xét ΔABC vuông tại A có 

\(\sin C=\dfrac{AB}{BC}\)

hay \(BC=16\sqrt{3}\left(cm\right)\)

=>\(AC=8\sqrt{3}\left(cm\right)\)

a: góc C=90-30=60 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin60=căn 3/2

=>BC=4*2/căn 3=8/căn 3(cm)

=>AC=4/căn 3(cm)

b: góc B=90-40=50 độ

Xét ΔABC vuông tại A có sin B=AC/BC

=>AC=6*sin50\(\simeq5\left(cm\right)\)

=>\(AB\simeq3,32\left(cm\right)\)

c: góc B=90-45=45 độ

Xét ΔABC vuông tại A có góc b=45 độ

nên AB=AC=4cm

=>BC=4căn 2(cm)