CHo U1 = 0 ; U2 = 1 và Un+1 = Un + Un-1
tính U3 ; U4
Những câu hỏi liên quan
Cho cấp số cộng
u
n
có
u
1
+
2
u
5
0
và
S
4
14
. Tính số hạng đầu
u
1
và công sai d của cấp số cộng. A.
u
1...
Đọc tiếp
Cho cấp số cộng u n có u 1 + 2 u 5 = 0 và S 4 = 14 . Tính số hạng đầu u 1 và công sai d của cấp số cộng.
A. u 1 = 8 ; d = 3
B. u 1 = - 8 ; d = 3
C. u 1 = - 8 ; d = - 3
D. u 1 = 8 ; d = - 3
Cho cấp số nhân
u
1
,
u
2
,
u
3
,
..
u
n
với công bội
q
q
≠
0
,
q
≠
1
.
Đặt
S
n
u...
Đọc tiếp
Cho cấp số nhân u 1 , u 2 , u 3 , .. u n với công bội q q ≠ 0 , q ≠ 1 . Đặt S n = u 1 + u 2 + u 3 + .. + u n . Khi đó ta có:
A. S n = u 1 q n − 1 q − 1
B. S n = u 1 q n − 1 − 1 q − 1
C. S n = u 1 q n + 1 q + 1
D. S n = u 1 q n − 1 − 1 q + 1
Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
Đúng 0
Bình luận (0)
Cho cấp số nhân
u
1
,
u
2
,
u
3
,
.
.
u
n
với công bội
q
(
q
≠
0...
Đọc tiếp
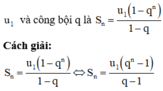
Cho cấp số nhân u 1 , u 2 , u 3 , . . u n với công bội q ( q ≠ 0 , q ≠ 1 ) . Đặt S n = u 1 + u 2 + u 3 + . . . + u n . Khi đó ta có:
A. S n = u 1 ( q n - 1 ) q - 1
B. S n = u 1 ( q n - 1 - 1 ) q - 1
C. S n = u 1 ( q n + 1 ) q + 1
D. S n = u 1 ( q n - 1 - 1 ) q + 1
Chọn A
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên
là u 1 và công bội q là S n = u 1 ( 1 - q n ) 1 - q
Cách giải:
S n = u 1 ( 1 - q n ) 1 - q ⇔ S n = u 1 ( q n - 1 ) q - 1
Đúng 0
Bình luận (0)
Cho CSC có: u1 + 2u5 = 0 và S4 = 14. Tính u10
=>u1+2(u1+4d)=0 và 4*(2u1+3d)/2=14
=>3u1+8d=0 và 2u1+3d=7
=>u1=8; d=-3
u10=u1+9d=8-27=-19
Đúng 1
Bình luận (0)
Cho CSN có: u1 + u3 + 3 và u12 +u32 = 5. 0<q<1. Tính S10
Cho cấp số nhân
u
n
với công bội q 0 và
u
2
4
;
u
4
9
. Tìm
u
1
. A.
u
1
-
8
3
B.
u
1...
Đọc tiếp
Cho cấp số nhân u n với công bội q < 0 và u 2 = 4 ; u 4 = 9 . Tìm u 1 .
A. u 1 = - 8 3
B. u 1 = 8 3
C. u 1 = - 6
D. u 1 = 6
Cho cấp số nhân
(
u
n
)
với công bội q 0 và
u
2
4
,
u
4
9
. Tìm
u
1
A.
u
1
−
8
3
.
B.
u
1
8...
Đọc tiếp
Cho cấp số nhân ( u n ) với công bội q < 0 và u 2 = 4 , u 4 = 9 . Tìm u 1
A. u 1 = − 8 3 .
B. u 1 = 8 3 .
C. u 1 = − 6.
D. u 1 = 6.
Vì q < 0 , u 2 > 0 nên u 3 < 0 .
Do đó u 3 = − u 2 . u 4 = − 4.9 = − 6
Ta có: u 2 2 = u 1 . u 3 ⇒ u 1 = u 2 2 u 3 = 4 2 − 6 = − 8 3 .
Chọn đáp án A
Đúng 0
Bình luận (0)
Dãy số
u
n
n
1
+
∞
là cấp số cộng, công sai d. Tổng
S
100
u
1
+
u
2
+
.
.
.
+
u
100
,
u...
Đọc tiếp
Dãy số u n n = 1 + ∞ là cấp số cộng, công sai d. Tổng S 100 = u 1 + u 2 + . . . + u 100 , u 1 ≠ 0 là
A. S 100 = 2 u 1 + 99 d
B. S 100 = 50 u 100
C. S 100 = 50 u 1 + u 100
D. S 100 = 100 u 1 + u 100
Cho cấp số nhân có u 1 < 0 và công bội q. Hỏi các số hạng khác sẽ mang dấu gì trong các trường hợp sau:
a. q > 0
b. q < 0
CSN (un) : un = u1.qn – 1, u1 < 0
a. q > 0 ⇒ qn – 1 > 0 ⇒ u1.qn – 1 < 0 (vì u1 < 0)
⇒ un < 0 với mọi n ∈ N*.
Vậy với q > 0 và u1 < 0 thì các số hạng đều mang dấu âm.
b. q < 0.
+ Nếu n chẵn ⇒ n – 1 lẻ ⇒ qn – 1 < 0
⇒ u1.qn – 1 > 0 (vì u1 < 0).
⇒ un > 0.
+ Nếu n lẻ ⇒ n – 1 chẵn ⇒ qn – 1 > 0
⇒ u1.qn – 1 < 0 (Vì u1 < 0).
⇒ un < 0.
Vậy nếu q < 0, u1 < 0 thì các số hạng thứ chẵn dương và các số hạng thứ lẻ âm.
Đúng 0
Bình luận (0)
Dãy số
(
u
n
)
n
1
+
∞
là cấp số cộng, công sai d. Tổng
S
100
u
1
+...
Đọc tiếp
Dãy số ( u n ) n = 1 + ∞ là cấp số cộng, công sai d. Tổng S 100 = u 1 + u 2 + . . . + u 100 , u 1 ≠ 0 là
A. S 100 = 2 u 1 + 99 d
B. S 100 = 50 u 100
C. S 100 = 50 u 1 + u 100
D. S 100 = 100 u 1 + u 100
Chọn C
Nếu ( u n ) n = 1 + ∞ là cấp số cộng có u 1 ≠ 0 và công sai d
thì S h = u 1 + u 2 + . . . + u n = n 2 u 1 + u n
Áp dụng với n=100, ta chọn C
Đúng 0
Bình luận (0)