4. Tính hiệu P(x)-Q(x) bằng hai cách ,trong đó: P(X)=6X³ +8x²+5x-2; Q(x)=-9x³ +6x² + 3+2x

Những câu hỏi liên quan
Tính hiệu P(x) – Q(x) bằng hai cách, trong đó:
\(\begin{array}{l}P(x) = 6{x^3} + 8{x^2} + 5x - 2;\\Q(x) = - 9{x^3} + 6{x^2} + 3 + 2x.\end{array}\)
Theo cột dọc:
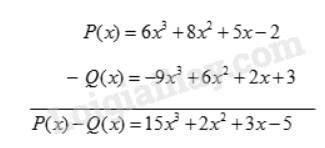
Theo hàng ngang:
\(\begin{array}{l}P(x) - Q(x) = 6{x^3} + 8{x^2} + 5x - 2 - ( - 9{x^3} + 6{x^2} + 2x + 3)\\ = 6{x^3} + 8{x^2} + 5x - 2 + 9{x^3} - 6{x^2} - 2x - 3\\ = (6 + 9){x^3} + (8 - 6){x^2} + (5 - 2)x + ( - 2 - 3)\\ = 15{x^3} + 2{x^2} + 3x - 5\end{array}\)
Đúng 0
Bình luận (0)
cho hai đa thức P(x) = 5x^3 -7 + 6x - 8x^3 - x^4 và Q(x)= -2x^3 + x^4 + 5 + 8x^3
a) sắp xếp các đa thức trên theo lũy thừa giảm dần của biến
b) tính M(x)=P(x)+Q(x)
c) tính giá trị của đa thức M(x) vừa tìm được tại x= -3
a) P(x) = -x4 - 3x3 + 6x - 7
Q(x) = x4 + 6x3 + 5
b) M(x) = P(x) + Q(x) = -x4 - 3x3 + 6x - 7 + (x4 + 6x3 + 5) = 3x3 + 6x - 2
c) M(-3) = 3.(-3)3 + 6.(-3) - 2 = -101
a) Sắp xếp P(x):-x4 - 3x3 + 6x - 7
Q(x) = x4 + 6x3 + 5
b) P(x) + Q(x) = (-x4- 3x3 + 6x - 7) + (x4 + 6x3 + 5)
= -x4 - 3x3 + 6x -7 + x4 + 6x3 + 5
= (-x4+ x4) + (-3x3 + 6x3) + 6x + (-7 + 5)
= 3x3 + 6x - 2
Vậy M(x) = 3x3 + 6x -2
c) Thay x = -3 vào biểu thức, ta có :
M(x) = 3(-3)3+ 6(-3) - 2
= -101
Hok tốt.
1)Cho các đa thức sau: f(x)=x^3-5x^2+8x-4 ; g(x)=x^3-3x+2 ; q(x)=x^3 - 5x^2+3x+9 ; h(x)=x^3+3^2+6x+4. Trong các giá trị x=+-1,x=+-2,x=+-3 giá trị nào là nghiệm của các đa thức đó
Phân tích đa thức thành nhân tử bằng cách tách hạng tử
\(x^2-6x+8\)
\(9x^2+6x-8\)
\(3x^2-8x+4\)
\(4x^2-4x-3\)
\(x^2-7x+12\)
\(x^2-5x-14\)
a) \(x^2-6x+8\)
\(=x^2-2\cdot x\cdot3+3^2-1\)
\(=\left(x-3\right)^2-1^2\)
\(=\left(x-3-1\right)\left(x-3+1\right)\)
\(=\left(x-4\right)\left(x-2\right)\)
Còn lại tương tự
Đúng 0
Bình luận (0)
a) \(x^2-6x+8=x^2-2x-4x+8\)
\(=\left(x^2-2x\right)-\left(4x-8\right)\)
=x(x-2)-4(x-2) = (x-2)(x-4)
Đúng 0
Bình luận (0)
mấy ý còn lại đợi xíu mk lm đã
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
P(x) =\(5x^2-7+6x-8x^3-x^4\)
Q(x)=\(x^4+5+8x^3-5x^2\)
a) sắp xếp 2 đa thức theo lũy thừa giảm dần của biến
b)tính P(x)+Q(x)
c)Tính P(x)-Q(x)
a) Ta có: \(P\left(x\right)=5x^2-7+6x-8x^3-x^4\)
\(=-x^4-8x^3+5x^2+6x-7\)
Ta có: \(Q\left(x\right)=x^4+5+8x^3-5x^2\)
\(=x^4+8x^3-5x^2+5\)
b) Ta có: P(x)+Q(x)
\(=-x^4-8x^3+5x^2+6x-7+x^4+8x^3-5x^2+5\)
\(=6x-2\)
c) Ta có: P(x)-Q(x)
\(=-x^4-8x^3+5x^2+6x-7-\left(x^4+8x^3-5x^2+5\right)\)
\(=-x^4-8x^3+5x^2+6x-7-x^4-8x^3+5x^2-5\)
\(=-2x^4-16x^3+10x^2+6x-12\)
Đúng 0
Bình luận (0)
câu a dễ bạn tự làm nha
b) Ta có: P(x)+Q(x)
=−x4−8x3+5x2+6x−7+x4+8x3−5x2+5=−x4−8x3+5x2+6x−7+x4+8x3−5x2+5
=6x−2=6x−2
c) Ta có: P(x)-Q(x)
=−x4−8x3+5x2+6x−7−(x4+8x3−5x2+5)=−x4−8x3+5x2+6x−7−(x4+8x3−5x2+5)
=−x4−8x3+5x2+6x−7−x4−8x3+5x2−5=−x4−8x3+5x2+6x−7−x4−8x3+5x2−5
=−2x4−16x3+10x2+6x−12
Đúng 0
Bình luận (0)
\(A\left(x\right)=-4x^5-x^3+4x^2+5x+9+4x^5-6x^2-2\)
\(B\left(x\right)=-3x^4-2x^3+10x^2-8x+5x^3-7-2x^3+8x\)
thu gọn đa thúc rồi sắp xếp theo thứ tự giảm dần của biến
tính A(x) + B(x) và A(x) - B(x)
Ta có: A(x) = -4x5 - x3 + 4x2 + 5x + 9 + 4x5 - 6x2 - 2
A(x) = (-4x5 + 4x5) - x3 + (4x2 - 6x2) + 5x + (9 - 2)
A(x) = -x3 - 2x2 + 5x + 7
B(x) = -3x4 - 2x3 + 10x2 - 8x + 5x3 - 7 - 2x3 + 8x
B(x) = -3x4 - (2x3 - 5x3 + 2x3) + 10x2 - (8x - 8x) - 7
B(x) = -3x4 + x3 + 10x2 - 7
Đúng 0
Bình luận (0)
A(x) + B(x) = (-x3 - 2x2 + 5x + 7) + (-3x4 + x3 + 10x2 - 7)
= -x3 - 2x2 + 5x + 7 - 3x4 + x3 + 10x2 - 7
= (-x3 + x3) - (2x2 - 10x2) + 5x + (7 - 7)
= 8x2 + 5x
A(x) - B(x) = (-x^3 - 2x^2 + 5x + 7) - (-3x^4 + x^3 + 10x^2 - 7)
= -x^3 - 2x^2 + 5x + 7 + 3x^4 - x^3 - 10x^2 + 7
= (-x^3 - x^3) - (2x^2 + 10x^2) + 5x + (7 + 7)
= -2x^3 - 12x^2 + 5x + 14
Đúng 0
Bình luận (0)
\(A\left(x\right)=-x^3-2x^2+5x+7\)
\(B\left(x\right)=-3x^4=x^3+10x^2-7\)
\(A\left(x\right)+B\left(x\right)=8x^2+5x\)
\(A\left(x\right)-B\left(x\right)=-2x^3-12x^2+5x+14\)
Đúng 0
Bình luận (0)
1. Các hằng đẳng thức sau là đúnga. x^2+6x+9/x^2+3x+3/x+1b. x^2-4/5x^2+13x+6x+2/5x+3c. x^2+5x+4/2x^2+x-3x^2+3x+4/2x^2-5x+3d. x^2-8x+16/16-x^24-x/4+x2. P là đa thức nào để x^2+2x+1/Px^2-1/4x^2-7x+3a. P4x^2+5x-2b. P4x^2+x-3c. P4x^2-x+3d. P4x^2+x+33. Đa thức Q trong đẳng thức 5(y-x)^2/5x^2-5xyx-y/Qa. x+yb. 5(x+y)c. 5(x-y)d. x4. Đa thức Q trong hằng đẳng x-2/2x^2+32x^2-4x/Q là:a. 4x^2+16b. 6x^2-4xc. 4x^3+6xd. khác5. Phân thức 2x+1/2x-3 bằng phân thức:a. 2x^2+x/2x-3b. 2x^2+x/2x^2-3xc. 2x+1/6x-9d. Khá...
Đọc tiếp
1. Các hằng đẳng thức sau là đúng
a. x^2+6x+9/x^2+3=x+3/x+1
b. x^2-4/5x^2+13x+6=x+2/5x+3
c. x^2+5x+4/2x^2+x-3=x^2+3x+4/2x^2-5x+3
d. x^2-8x+16/16-x^2=4-x/4+x
2. P là đa thức nào để x^2+2x+1/P=x^2-1/4x^2-7x+3
a. P=4x^2+5x-2
b. P=4x^2+x-3
c. P=4x^2-x+3
d. P=4x^2+x+3
3. Đa thức Q trong đẳng thức 5(y-x)^2/5x^2-5xy=x-y/Q
a. x+y
b. 5(x+y)
c. 5(x-y)
d. x
4. Đa thức Q trong hằng đẳng x-2/2x^2+3=2x^2-4x/Q là:
a. 4x^2+16
b. 6x^2-4x
c. 4x^3+6x
d. khác
5. Phân thức 2x+1/2x-3 bằng phân thức:
a. 2x^2+x/2x-3
b. 2x^2+x/2x^2-3x
c. 2x+1/6x-9
d. Khác
Câu 5:B
Câu 4: C
Câu 3: D
Câu 2: A
Câu 1: A
Đúng 0
Bình luận (0)
Cho f(x)=\(\left(8x^2+5x-14\right)^{2015}.\left(3x^3-10x^2+6x+2\right)^{2016}\)
Sau khi thu gọn thì tính tổng các hệ số của f(x) là bao nhiêu?
gợi ý: tổng các hệ số trong đa thức 1 biến bằng giá trị của đa thức đó tại giá trị của biến bằng 1
Tổng các hệ số của 1 đa thức f(x) bất kì bằng giá trị của đa thức đó tại x=1
Vậy tổng các hệ số của đa thức
f(x)=(8x2+5x-14)2015.(3x3-10x2+6x+2)2016
=f(1)=(8.12+5.1-14)2015.(3.13-10.12+6.1+2)2016=(-1)2015.12016=(-1).1=-1
Đúng 1
Bình luận (0)
tính giá trị biểu thức bằng cách hợp lí
3x^2. ( 5x^2 - 4 ) + x^2 (8-15x^2)-8x với x= /3/























