Cho hai góc lượng giác có sđ O x , O u = - 5 π 2 + m 2 π và sđ O x ; O v = - π 2 + n 2 π . Khẳng định nào sau đây đúng?
A. Ou và Ov trùng nhau.
B. Ou và Ov đối nhau.
C. Ou và Ov vuông góc.
D. Tạo với nhau một góc π/4.
Chọn A.
Ta có: 
Vậy n = m-1 do đó Ou và Ov trùng nhau.
Nếu góc lượng giác sđ ( Ox; Oz) =- 63 pi / 12 = - 63 π 12 có thì hai tia Ox và Oz
Cho hai góc lượng giác có số đo O x ; O u = 5 π 2 + 2 m π
A.
cho đường tròn (O) và dây EF. qua O kẻ tia Ox vuông góc với EF tại I, cắt đường tròn tại D, và cắt tiếp tuyến tại E ở C.
a)chứng minh: CF là tiếp tuyến của đường tròn.
b) cho bán kín đường tròn(O) =15cm, dây EF=24cm. tính góc ECF
Gợi ý: a) CM: tam giác OEF cân tại O => góc EOI=góc IOF? =>tam giác EOC =tam giác FOC
b) sử dụng hệ thức lượng giác trong tam giác vuông, tính góc EOI từ tam giác IOE=>sđ góc ECF
Cho sđ (Ox, Ou)=-260°; sđ(Ox, Ov)= 150°. Tính sđ (Ou, Ov)
\(sđ\left(Ou;Ov\right)=sđ\left(Ox;Ov\right)-sđ\left(Ox;Ou\right)\)
\(=150^0-\left(-260^0\right)+k\cdot360^0\)
\(=410^0+k\cdot360^0\)
\(=50^0+\left(k-1\right)\cdot360^0\)
Cho sđ(Ox, Ou)=-260°; sđ(Ox, Ov)=150°. Tính sđ(Ou,Ov)
\(sđ\left(Ox;Ou\right)=-260^o=-260^o+360^o=100^0\)
mà \(sđ\left(Ox;Ov\right)=150^o\)
\(\Rightarrow sđ\left(Ou;Ov\right)=150^o-100^0=50^0\)
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho sđ A B ⏜ = 60 o , sđ B C ⏜ = 90 o , sđ C D ⏜ = 120 o
Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
Nếu góc lượng giác có s đ O x , O z = - 63 π 2 thì hai tia Ox và Oz
A. Trùng nhau.
B. Vuông góc.
C. Tạo với nhau một góc bằng 3π/4.
D. Đối nhau.
Chọn B.
Ta có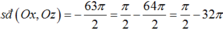 
Suy ra : hai tia Ox và Oz vuông góc với nhau.
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D .
a) Tính sđ góc BOC và sđ cung nhỏ AC .
b) chứng minh tứ giác OBDC nội tiếp .
c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE .
d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
