\(a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}BM=MC\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BCD}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}CD\\ c,\left\{{}\begin{matrix}BM=MC\\\widehat{AMC}=\widehat{BMD}\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow\widehat{ACB}=\widehat{CBD}\\ \text{Mà 2 góc này ở vị trí slt nên }AC\text{//}BD\)

BÀI NÀY ĐÂU KHÓ 

Xét \(\Delta AMB\)VÀ \(\Delta AMC\)

                                                                                                                                                  AB=AC(gt)

                                                                                                                                        <B=<C(tam giác ABC cân)

                                                                                                                                           BM=MC(gt)

                                                                                                                          \(\Rightarrow\Delta AMB=\Delta AMC\left(c-g-c\right)\)

                                                            Xét \(\Delta AMB\)và\(\Delta CMD\)có:

                                                                <AMB=<CMD(đối đỉnh)

                                                                AM=MD(gt)

                                                                 MB=MC(gt)

                                                    \(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)

                                                   =>góc BAM=<CDM(2 góc tương ướng)

                                   mà hai góc này ở vị trí so le trong

                        => AB//CD

Khiếp, bạn gõ lại cẩn thận từng chữ được không ạ?

a) Sửa đề: ΔAMB=ΔDMC

Xét ΔAMB và ΔDMC có 

MA=MD(gt)

\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)

MB=MC(M là trung điểm của BC)

Do đó: ΔAMB=ΔDMC(c-g-c)

1.

Xét tam giác AMB và tam giác NMC có:

AM = NM (gt)

AMB = NMC (2 góc đối đỉnh)

MB = MC (M là trung điểm của BC)

=> Tam giác AMB = Tam giác NMC (c.g.c)

Xét tam giác AMC và tam giác NMB có:

AM = NM (gt)

AMC = NMB (2 góc đối đỉnh)

MC = MB (M là trung điểm của BC)

=> Tam giác AMC = Tam giác NMB (c.g.c)

2.

Xét tam giác AME và tam giác BMC có:

AM = BM (M là trung điểm của AB)

AME = BMC (2 góc đối đỉnh)

ME = MC (gt)

=> Tam giác AME = Tam giác BMC (c.g.c)

=> AEM = BCM (2 góc tương ứng)

mà 2 góc này ở vị trí so le trong

=> AE // BC

Xét tam giác ANF và tam giác CNB có:

AN = CN (N là trung điểm của AC)

ANF = CNB (2 góc đối đỉnh)

NF = NB (gt)

=> Tam giác ANF = Tam giác CNB (c.g.c)

=> AF = CB (2 cạnh tương ứng)

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

c: Xét ΔMAB vuông tại M và ΔMDC vuông tại M có

MA=MD

MB=MC

Do đó: ΔMAB=ΔMDC

=>\(\widehat{MAB}=\widehat{MDC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD

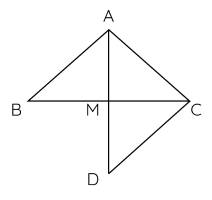
a) Xét hai tam giác $AMB$ và $AMC$ có:

$AM$ là cạnh chung;

$AB = AC$ (gt);

$BM = MC$ ($M$ là trung điểm $BC$);

Suy ra $\Delta AMB=\Delta AMC$ (c.c.c)

b) $\Delta AMB=\Delta AMC$ suy ra

$\widehat{BAM} = \widehat{CAM}$ (hai góc tương ứng)

Suy ra $AM$ là tia phân giác của góc $BAC$.

c) Xét hai tam giác $AMD$ và $DMC$ có:

$AM = AD$ (gt);

$\widehat{AMB} = \widehat{CMD}$ (hai góc đối đỉnh);

$BM = MC$.

Nên $\Delta AMD=\Delta DMC$ (c.g.c)

Suy ra $\widehat{BAM} = \widehat{CDM}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên $AB$ // $CD$.

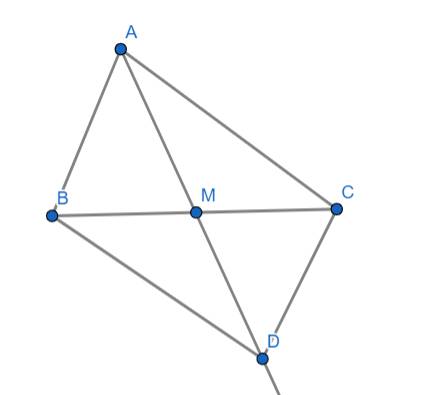
a) Xét ΔAMB và ΔDMC có:

\(AM=CM\) (gt) 

\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh) 

\(BM=CM\) (M là trung điểm của BC) 

\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)

b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)

\(\Rightarrow AB=DC\) (2 cạnh t.ứng)  

c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)

\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng) 

Mà hai góc này ở vị trí so le trong 

\(\Rightarrow AB//CD\)

a,Có BC^2=5^2=25 
AB^2+AC^2=3^2+4^2=25 
suy ra BC^2=AB^2+AC^2 
Theo ĐL Pitago đảo thì tam giác ABC vuông tại A. 

B) Xét \(\Delta ABM\)và \(\Delta CDM\) có:

   \(\hept{\begin{cases}DM=BM\left(gt\right)\\AM=CM\left(gt\right)\\\widehat{BMA}=\widehat{CMD}\left(2gocdoidinh\right)\end{cases}\Rightarrow\Delta ABM=\Delta CDM\left(c-g-c\right)}\)

\(\Rightarrow\widehat{ABM}=\widehat{MCD}\)mà \(\widehat{ABM}=90^0\left(cmt\right)\)

\(\Rightarrow\widehat{MCD}=90^0\)

\(\Rightarrow AC\perp CD\left(đpcm\right)\)