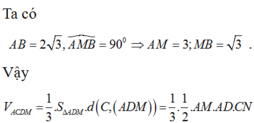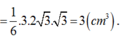Cho(O) đường kính AB; I là trung điểm của OB, Qua I kể dây CD vuông góc với dây AB,kể dây CE//AB. a) Chứng minh : AE=BC=BD b) chứng minh :E, O,D thẳng hàng. C) chứng minh :tứ giác ADBE là hình chữ nhật

Những câu hỏi liên quan
Bài 1:Cho (O,5cm ) đường kính AB .Trên AB lấy điểm H sao cho AH2cm. Vẽ dây CD vuông góc AB tại H . Gọi K là điểm đối xứng của A qua H a) Chứng minh ◇ACKD là hình thoi.b)Gọi I là giao điểm của DK và BC.Vẽ đường tròn tâm O đường kính AB . Chứng minh rằng đường tròn này đi qua I.c)Chứng minh góc HIO90°d) Tính IH?
Đọc tiếp
Bài 1:Cho (O,5cm ) đường kính AB .Trên AB lấy điểm H sao cho AH=2cm. Vẽ dây CD vuông góc AB tại H . Gọi K là điểm đối xứng của A qua H
a) Chứng minh ◇ACKD là hình thoi.
b)Gọi I là giao điểm của DK và BC.Vẽ đường tròn tâm O' đường kính AB . Chứng minh rằng đường tròn này đi qua I.
c)Chứng minh góc HIO=90°
d) Tính IH?
Cho nửa đường tròn tâm (O),đường kính AB 2R.Vẽ bán kính OC vuông góc với AB. Lấy điểm K bất kì thuộc cung AC, kẻ KH vuông gócvới AB tại H. Tia AC cắt HK tại I, tia BI cắt nửa tròn tại điểm E.1) Chứng minh tứ giác BHIC nội tiếp;2) Chứng minhAI.AC AH. AB và tổng AI.AC +BI.BE không đổi.3) Chứng minh HE vuông góc với CEvà tâm đường tròn ngoại tiếp tam giác CEH nằm trên đường thẳng cố định khi K di động trên cung AC.
Đọc tiếp
Cho nửa đường tròn tâm (O),đường kính AB = 2R.Vẽ bán kính OC vuông góc với AB. Lấy điểm K bất kì thuộc cung AC, kẻ KH vuông gócvới AB tại H. Tia AC cắt HK tại I, tia BI cắt nửa tròn tại điểm E.
1) Chứng minh tứ giác BHIC nội tiếp;
2) Chứng minhAI.AC = AH. AB và tổng AI.AC +BI.BE không đổi.
3) Chứng minh HE vuông góc với CEvà tâm đường tròn ngoại tiếp tam giác CEH nằm trên đường thẳng cố định khi K di động trên cung AC.
1) AB là đường kính \(\Rightarrow\angle ACB=90\) mà \(\angle IHB=90\Rightarrow BHIC\) nội tiếp
2) Xét \(\Delta AHI\) và \(\Delta ACB:\) Ta có: \(\left\{{}\begin{matrix}\angle AHI=\angle ACB=90\\\angle CABchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHI\sim\Delta ACB\left(g-g\right)\Rightarrow\dfrac{AI}{AH}=\dfrac{AB}{AC}\Rightarrow AI.AC=AB.AH\)
Tương tự \(\Rightarrow\Delta BIH\sim\Delta BAE\Rightarrow\dfrac{BI}{BH}=\dfrac{BA}{BE}\Rightarrow BI.BE=BA.BH\)
\(\Rightarrow AI.AC+BI.BE=AH.AB+BH.AB=AB\left(AH+BH\right)\)
\(=AB^2=4R^2\)
3) Xét \(\Delta CAB\): Ta có: \(\left\{{}\begin{matrix}\angle ACB=90\\AO=OB\\CO\bot AB\end{matrix}\right.\Rightarrow\Delta CAB\) vuông cân tại C
\(\Rightarrow\) C cố định
Ta có: \(\angle ECO+\angle EHO=90+\angle ECA+\angle ACO+\angle EHI\)
\(90+\angle EBA+\angle CAO+\angle IAE=90+\angle EAB+\angle EBA=180\)
\(\Rightarrow CEHO\) nội tiếp mà \(\angle HOC=90\Rightarrow\angle HEC=90\Rightarrow HE\bot EC\)
Vì \(CEHO\) nội tiếp \(\Rightarrow\) tâm của (CEH) là tâm của (CEHO)
\(\Rightarrow\) tâm của (CEH) thuộc trung trực CO mà C,O cố định
\(\Rightarrow\) đpcm
Đúng 3
Bình luận (1)
Cho nửa đường tròn (O) đường kính AB. Lấy M∈OA, N∈nửa đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua N và vuông góc với NM cắt Ax tại C, cắt By tại D. Gọi I là giao điểm của AN và CM, K là giao điểm của BN và DM. Chứng minh IK //AB.
△AMB nội tiếp đường tròn đường kính AB nên △AMB vuông tại M.
- Ta có: \(\widehat{CAB}+\widehat{DBA}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{CAM}+\widehat{MAB}+\widehat{DBM}+\widehat{MBA}=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+90^0=180^0\) nên \(\widehat{CAM}+\widehat{DBM}=90^0\)
Tứ giác ANMC có: \(\widehat{NAC}+\widehat{NMC}=90^0+90^0=180^0\)
Nên tứ giác ANMC nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CNM}\)
Tứ giác BNMD có: \(\widehat{NBD}+\widehat{NMD}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác BNMD nội tiếp \(\Rightarrow\widehat{MBD}=\widehat{MND}\)
\(\Rightarrow\widehat{CNM}+\widehat{MND}=\widehat{CAM}+\widehat{MBD}=90^0\)
\(\Rightarrow\widehat{INK}=90^0\).
Tứ giác MINK có: \(\widehat{IMK}+\widehat{INK}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác MINK nội tiếp nên \(\widehat{MIK}=\widehat{MNK}\)
Lại có \(\widehat{MNK}=\widehat{MBD}\left(cmt\right)\) \(\Rightarrow\widehat{MIK}=\widehat{MBD}\)
Xét (O): \(\widehat{MBD}=\widehat{MAB}\left(=\dfrac{1}{2}sđ\stackrel\frown{MB}\right)\)
\(\Rightarrow\widehat{MIK}=\widehat{MAB}\) nên IK//AB
Đúng 2
Bình luận (2)
Giúp mik giải
Cho 2 điểm phân biệt A,B tìm quỹ tích điểm M thỏa mãn vectơ AM× vectơ AB =AM^2
A Đường trung trực của đoạn AB
B Đường tròn đường kính AB
C Đường tròn tâm A bán kính AB
D đường thẳng qua A và vuông góc với AB
Xem chi tiết
\(\overrightarrow{AM}.\overrightarrow{AB}=AM^2=\overrightarrow{AM}^2\)
\(\Leftrightarrow\overrightarrow{AM}\left(\overrightarrow{AB}-\overrightarrow{AM}\right)=0\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{MB}=0\)
\(\Rightarrow AM\perp BM\)
\(\Rightarrow\) Quỹ tích là đường tròn đường kính AB
Đúng 0
Bình luận (0)
1,cho tam giác ABC nội tiếp (O). Vẽ các đường kính AD, BE, CF. Gọi M, N, P lần lượt là trung điểm BC, CA, AB cmr DM, EN, FP đồng quy
2,Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi H là giao điểm của đường trung tuyến CM với OA. Gọi G là trọng tâm của tam giác AMC. CMR:a) OM vuông góc GHb) OG vuông góc CM
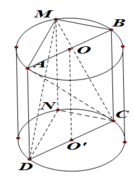
Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh
2
3
với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung
A
B
⏜
của đường tròn đáy sao cho
A
B
M
⏜
60
0
. Thể tích của khối tứ diện ACDM là:
Đọc tiếp
Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2 3 với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung A B ⏜ của đường tròn đáy sao cho A B M ⏜ = 60 0 . Thể tích của khối tứ diện ACDM là:
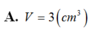
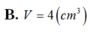
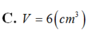
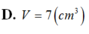
Cho đường tròn tâm O đường kính AB.M,N thuộc AB sao cho OM=ON.I là 1 điểm thuộc đường tròn.IM,IN cắt (O) tại D,E.IO cắt (O) tại Q.DE cắt AB tại K.chứng minh rằng KQ là tiếp tuyến của đường tròn
Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kính BA, chúng cắt nhau ở C và D. Chứng minh CD là đường trung trực của AB:/
Xem chi tiết
Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB. Trên nửa đường tròn lấy 5 điểm C1,C2,C3,C4,C5. Cứ qua 2 điểm vẽ 1 đường thẳng. Hỏi có bao nhiêu tam giác tạo thành có 3 đỉnh là 3 trong các điểm đã cho?
Các bạn chỉ cần định hướng cách làm cho mình thui!
Bạn nào giúp mình sớm nhất, mình tick cho!!!
vi lay tren duong tron 5 diem phan biet nen 5 diem nay ko thang hang
Suy ra so tam giac moi tao thanh =5x4x3=60 tam giac
tuy nhien moi dinh lai duoc lap lai 2 lan nen chi co 60 : (2x3) = 10 tam giac
Vay co 10 tam giac co 3 dinh la 3 trong cac diem da cho
Đúng 0
Bình luận (0)
Mình vẫn ko hiểu rõ ý tưởng của bạn lắm, các bạn có thể giải rõ ràng hơn đc ko! Thank nhìu nha!
Đúng 0
Bình luận (0)
ban dua vao cong thuc nay nek neu n diem pha biet ko thang hang thi se co n(n-1)/2
boi vi tu 1 diem ta se noi duoc voi n-1 diem con lai ma co n diem nen co n(n-1)
tuy nhien 1 diem da bi lap lai 1 lan nen ta chi co n(n-1)/2 doan thang ma thoi
doi voi bai tam giac thi n = 5 con so lan cac diem lap lai la 3 x2 = 6 lan nen co n(n-1)(n-2)/6
neu ban van chua hieu thi nt mik nha
Đúng 0
Bình luận (0)
Cho đường tròn (O; R), đường kính AB. Lấy điểm C thuộc đường tròn (O; R) (AC BC). Kẻ đường cao CH của tam giác ABC ( H thuộc AB ), kéo dài CH cắt (O; R) tại điểm D ( D khác C ). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường trón (O;R) giao nhau tại điểm M. Gọi I là giao điểm của OM và AC, hai đường MC và AB cắt nhau tại F.C/m AF.BHBF.AH
Đọc tiếp
Cho đường tròn (O; R), đường kính AB. Lấy điểm C thuộc đường tròn (O; R) (AC > BC). Kẻ đường cao CH của tam giác ABC ( H thuộc AB ), kéo dài CH cắt (O; R) tại điểm D ( D khác C ). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường trón (O;R) giao nhau tại điểm M. Gọi I là giao điểm của OM và AC, hai đường MC và AB cắt nhau tại F.C/m AF.BH=BF.AH