Cho ΔABC có AB= \(a\sqrt{5}\) ; BC= \(a\sqrt{3}\) ; AC= \(a\sqrt{2}\).
a) CM: ΔABC vuông tại C
b) Tính các tỉ số lượng giác của góc B, từ đó suy ra tỉ số lượng giác của góc A.
Mong mn giúp mik
Những câu hỏi liên quan
30 tháng 4 2023 lúc 20:53
Cho ΔABC vuông tại A có AB=5;AC=4.Bán kính đường tròn qua A và tiếp xúc với BC tại B bằng
A.\(\dfrac{5}{4}\sqrt{41}\) B.\(\dfrac{5}{2}\sqrt{41}\) C.\(\sqrt{41}\) D.\(\dfrac{5}{8}\sqrt{41}\)
Cho ΔABC vuông tại A có góc C =60 , AB=\(\sqrt{192}\)cm.
Diện tích của ΔABC là \(\sqrt{a}cm^2\) . Vậy a =
a)Cho ΔABC có a=5,b=6,góc ACB=30 độ.Tính cạnh AB
b)Cho ΔABC cân tại A,có cạnh AB=a.Tính số đo các cạnh,các góc còn lại của ΔABC và tính bán kính đường tròn ngoại tiếp ΔABC biết góc A=70 độ
Cho ΔABC vuông tại A có góc C = 60 độ , AB= \(\sqrt{192}\)cm.
Diện tích của ΔABC là \(\sqrt{a}\).cm Vậy a =
20 tháng 4 2023 lúc 9:07
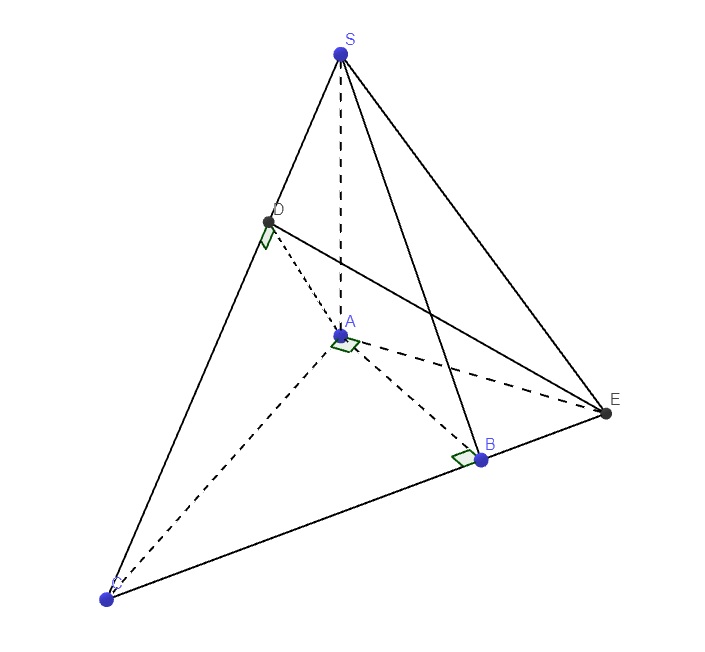
Cho hình chóp S.ABC có SA vuông góc (ABC), đáy là ΔABC vuông tại B, AB=a, \(BC=a\sqrt{3}\), \(SA=\dfrac{a\sqrt{6}}{2}\). Tính góc((SAC);(SBC))
Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A có góc C = 60 độ , AB= căn 192 cm.
Diện tích của ΔABC là \(\sqrt{a}\)cm2 . Vậy a =?
Kẻ AH vuông góc với BC
Có: A + B + C = 1800 => B = 180 - (A + C) = 180- (90 - 60) = 300
Trong tam giác AHB có: AH là đường cao và góc ABH = 300
=> tam giác AHB là 1/2 tam giác đều
=> BH = \(\frac{AB\sqrt{3}}{2}=\frac{\sqrt{192}.\sqrt{3}}{2}=12cm\)
và AH = 1/2.AB = 1/2.\(\sqrt{192}\) = \(4\sqrt{3}cm\)
Có: AH2 = HB.HC => HC = \(\frac{AH^2}{HB}=\frac{\left(4\sqrt{3}\right)^2}{12}=4cm\)
=> BC = HB + HC = 12 + 4 = 16cm
Diên tích của tam giác ABC: \(S_{ABC}=\frac{AH.BC}{2}=\frac{4\sqrt{3}.16}{2}=32\sqrt{3}cm^2=\sqrt{a}\Rightarrow a=\left(32\sqrt{3}\right)^2=3072\)
Vậy a = 3072
Đúng 0
Bình luận (0)
24 tháng 2 2023 lúc 21:56
Cho ΔABC cân tại A,I là giao điểm của hai đường phân giác trong.Biết IB=3;IA=\(3\sqrt{6}\).Độ dài cạnh AB là
A.\(5\sqrt{3}\) B.\(\dfrac{3\sqrt{17}}{2}\) C.\(3\sqrt{19}\) D.3\(\sqrt{10}\)
Cho ΔABC có AB = 4cm, AC= 6cm, BC= \(2\sqrt{13}\) cm.
Chứng minh : AB.sinB = AC. SinC
Ta có:
\(AB^2=4^2=16\)
\(AC^2=6^2=36\)
\(BC^2=\left(2\sqrt{13}\right)^2=52\)
\(\Rightarrow AB^2+AC^2=BC^2\left(=52\right)\)
\(\Rightarrow\Delta ABC\) vuông tại A (theo định lý Pytago đảo)
\(\Rightarrow sinB=\dfrac{AC}{BC}\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow\dfrac{sinB}{sinC}=\dfrac{\dfrac{AC}{BC}}{\dfrac{AB}{BC}}=\dfrac{AC}{AB}\)
\(\Rightarrow AB.sinB=AC.sinC\)
Đúng 1
Bình luận (0)
cho ΔABC có AB=c, BC=a, CA=b. diện tích ΔABC là 5 cm2. tìm GTNN của biểu thức a2+2b2+3c2
11 tháng 1 2023 lúc 19:57
Cho ΔABC cân tại A.I là giao điểm của hai đường phân giác trong.Biết IB=3;IA=\(3\sqrt{6}\).Độ dài cạnh AB là
A.5\(5\sqrt{3}\) B.\(3\sqrt{19}\) C.\(3\sqrt{10}\) D.\(\dfrac{3\sqrt{17}}{2}\)