Tam giác ABC có góc A nhỏ hơn 90 độ vẽ ra phía ngoài tam giác đó AD vuông AB; AD =AB, AE vuông góc với AC , E=AC CMR:
a, DC=BE
b, BCvuông BE
Tam giác ABC có góc A nhỏ hơn 90 độ vẽ ra phía ngoài tam giác đó AD vuông AB; AD =AB, AE vuông góc với AC , E=AC CMR:
a, DC=BE
b, BCvuông BE
(mọi người trả lời nhanh giúp nha ! )
a)
Ta có :
\(\widehat{DAC}=\widehat{EAB}\left(=90^0+\widehat{BAC}\right)\)
=> \(\Delta DAC=\Delta EAB\left(c.g.c\right)\)
=> DC = EB ( hai cạnh tương ứng )
b)
Gọi giao điểm của DC với BE ; BA lần lượt là H và I
Vì \(\Delta DAC=\Delta EAB\)(c/m câu a)
=> \(\widehat{DAI}=\widehat{IBH}\)
Mà \(\widehat{DIA}=\widehat{HIB}\)( đối đnhr )
=> \(\widehat{DAI}=\widehat{IHB}=90^0\)
a) Xét \(\Delta ADC,\Delta ABE\) có:
AD = AB ( gt )
\(\widehat{DAC}=\widehat{EAB}\left(=90^o+\widehat{BAC}\right)\)
AE = AC ( gt )
\(\Rightarrow\Delta DAC=\Delta EAB\left(c-g-c\right)\)
\(\Rightarrow DC=BE\) ( 2 cạnh tương ứng ) ( đpcm )
b) Gọi giao điểm giữa DC và AB là K
giao điểm giữa DC và BE là M
Ta có: \(\widehat{ADK}+\widehat{K_1}=90^o\) ( do \(\Delta DAK\) có \(\widehat{DAK}=90^o\) ) (1)
Vì \(\Delta ADC=ABE\)
\(\Rightarrow\widehat{ADC}=\widehat{ABE}\) ( 2 góc tương ứng )
hay \(\widehat{ADK}=\widehat{KBE}\) (2)
Mà \(\widehat{K_1}=\widehat{K_2}\) ( đối đỉnh ) (3)
Xét (1), (2) và (3) ta có:
\(\widehat{ADK}+\widehat{K_1}=90^o\)
Mà \(\widehat{ADK}=\widehat{KBE}\)
\(\widehat{K_1}=\widehat{K_2}\)
\(\Rightarrow\widehat{KBE}+\widehat{K_2}=90^o\)
Xét \(\Delta KBM\) có \(\widehat{KBE}+\widehat{K_2}=90^o\Rightarrow\widehat{KMB}=90^o\)
\(\Rightarrow BE\perp DC\left(đpcm\right)\)
Cho tam giác ABC có góc A nhỏ hơn 90 độ . Vẽ ra phía ngoài của tam giác đó hai đoạn thẳng AD vuông góc và bằng AB ; AE vuông góc và bằng AC . Gọi H là trung điểm của BC .
Chứng minh rằng tia HA vuông góc với DE
Cho tam giác ABC có góc A bé hơn 90 độ. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng: AD vuông góc và bằng AB, AE vuông góc và bằng AC. Chứng minh DC=BE và DC vuông góc với BE
a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE
Các bn xem thử đúng ko nhé , mai mk kiểm tra 45' , cần ý kiến gấp
a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...
Tam giác ABC có \(\widehat{A}\) nhỏ hơn 90 độ vẽ ra phía ngoài tam giác đó AD vuông AB; AD =AB, AE vuông góc với AC , AE=AC .Gọi H là chân đường vuông góc kẻ từ A đến BC .Chứng minh tia HA đi qua trung điểm của đoạn thẳng DE
\(\sqrt{\sqrt[]{}\frac{ }{ }\hept{\begin{cases}\\\end{cases}}\hept{\begin{cases}\\\\\end{cases}}^{ }\orbr{\begin{cases}\\\end{cases}}_{ }_{ }^2\widehat{ }\widebat{ }\overline{ }\overrightarrow{ }^{ }_{ }\underrightarrow{ }|^{ }_{ }\cot\sin\cos\tan\sinh\cosh\tanh\Leftrightarrow}\)
Bạn chat gì linh tinh vậy???
cho tam giác ABC có góc a nhỏ hơn 90 độ. vẽ ra phía ngoài tam giác 2 đoạn thẳng AD vuông góc và bằng AB , AE vuông góc và bằng AC . H là chân đường từ A đến BC . CM AH là đường đi qua trung điểm của DE
Tự vẽ hình nha!~Giải:
Kẻ AH cắt DE tại F
Trên tia đối HA lấy N sao cho HA = HN
Ta có : AN cắt BC tại H
Mà H là trung điểm của AN và BC
=> Tứ giác ACNB là hình bình hành
=> AB // CN và CN = AB = AD
Ta có : góc DAE + góc EAC + góc DAB + góc BAC
= 360*.gócDAE + góc EAC + góc DAB + góc BAC = 360*
=> góc DAE + góc BAC = 360* - góc EAC - góc DAB
= 360* - 90* - 90*
= 180*.góc DAE + góc BAC
= 360* - góc EAC - góc DAB
= 360* - 90* - 90* 180*
Mà góc ACN + góc BAC = 180*. góc ACN + góc BAC = 180* (góc trong cùng phía )
=> góc DAE = góc ACN + góc DAE = góc ACN
Xét ΔDAE và ΔNCA có:
AE = AC
góc DAE = góc ACN
AD = CN
=> Vậy ΔDAE = ΔNCA (c.g.c)
Ta có: góc FAE + góc EAC + góc CAH = 180*
<=> góc FAE + góc CAH = 180* - góc EAC
= 180* − 90* = 90*
Mà góc CAH = góc FEA ( vì ΔDAE = ΔNCA)
góc FAE + góc FEA = 90*
=> ΔAEF ⊥ tại F
=> AH ⊥ DE (đpcm)
Vẽ mãi cho bạn nè!~
Kết bạn!`Tích giùm mink nha!~
Cho tam giác ABC có góc A < 90 độ. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD vuông góc và bằng AB; AE vuông góc và bằng AC.Chứng minh: DC=BE VÀ BC vuông góc với BE
a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...
Cho tam giác ABC có góc A nhỏ hơn 90 độ. Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân đỉnh A là MAB và NAC
a) Chứng minh MC = NB
b) Chứng minh MC vuông góc NB
giúp mik với
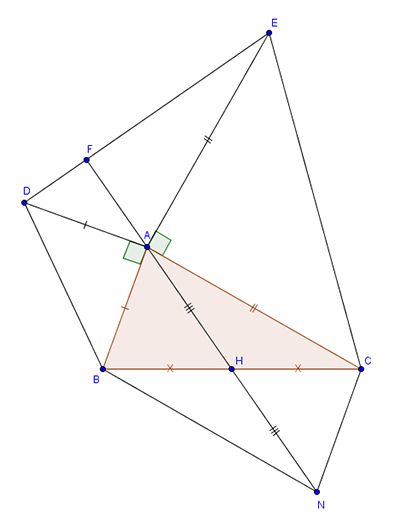
cho tam giac ABC có góc A nhỏ hơn 90 độ. Vẽ ra phía ngoài tam giác đó 2 đoạn thẳng AD vuông góc và bằng AB;AE vuông góc và băng AC
a)C/m DC=BE;DCvuông góc với BE
b)Gọi N là trung điểm của DE.Trên tia đối NA lấy M sao cho NA=NM
C/m AB=ME;Tam giác ABC=Tam giác EMA
c)C/M:MA vuông góc với BC
a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE
Cho tam giác ABC có góc B và góc C nhỏ hơn 90 độ. Vẽ ra phía ngoài của tam giác ấy các tam giác vuông cân ABD, ACE(trong đó ABD và ACE đều bằng 90 độ) Vẽ tia DI và EK cùng vuông góc với BC. Chứng minh rằng BC = DI + KE