Cho tam giác ABC gọi M, N, P lần lượt là trung điểm của ba cạnh AB; AC và BC. Gọi I là giao điểm của AP và MN
a) Chứng minh MN song song BC
b) Chứng minh IA = IP
Những câu hỏi liên quan
22 tháng 9 2021 lúc 19:38
Bài 5: Cho tam giác ABC vuông tại A,AB12 cm BC13 cm .Gọi M, N lần lượt là trungđiểm của AB và BCa) Chứng minhMN vuông góc AB b) Tính độ dài MNBài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi Ilà giao điểm của AP và MN. C/m: a) IA IP b) IM IN.Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểmcủa DH, M là trung điểm của HC.C/m:a) IM vuông góc AD b) AI vuông góc DM.
Đọc tiếp
Bài 5: Cho tam giác ABC vuông tại A,
AB=12 cm BC=13 cm .
Gọi M, N lần lượt là trung
điểm của AB và BC
a) Chứng minh
MN vuông góc AB
b) Tính độ dài MN
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểm
của DH, M là trung điểm của HC.
C/m:a) IM vuông góc AD b) AI vuông góc DM.
Câu 1. Cho tam giác ABC. Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Gọi M, N, P lần lượt là hình chiếu O trên các cạnh AB, BC, CA. Biết AB > BC > CA. Khi đó:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC và BC. Gọi I là giao điểm của AP và MN. Chứng minh IA = IP; IM = IN.
M là trung điểm của AB
N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> MN // BC
mà N là trung điểm của AC
=> I là trung điểm của AP
=> IA = IP
bạn tham khảo nha
Đúng 2
Bình luận (2)
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm của BD và N là trung điểm của EC. Chứng minh ba điểm E, A, D thẳng hàng.
23 tháng 9 2021 lúc 10:56
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
mọi người ơi giúp mình bài này với mình cần gấp bài này
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lần lượt lấy các điểm D và E
sao cho AD = AE. Gọi M là trung điểm của đoạn thẳng BC, gọi N là trung điểm của đoạn
thẳng DE. Chứng minh :
a) tgABC =tgACB
b) DE // BC
c) Ba điểm A, M, N là ba điểm thẳng hàng.
a: Xét ΔABC có
AD/AB=AE/AC
Do đó: DE//BC
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC, PO vuông góc với AC.
Tham khảo:
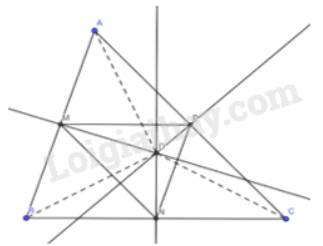
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC
Đúng 0
Bình luận (0)
Cho tam giác ABC. gọi M, N , P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I là giao điểm của AP và MN
a) chứng minh IA=IP
b) chứng minh IM =IN
c) Biết chu vi của tam giác ABC là 54cm. tính chu vi tam giác MNP
Bài 3: Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD = AE. Gọi M là trung điểm của đoạn thẳng BC, gọi N là trung điểm của đoạn thẳng DE. Chứng minh :
a) ABC =ACB
b) DE // BC
c) Ba điểm A, M, N là ba điểm thẳng hàng.