Tìm x biết x 2 + 1, x − 2,1 − 3 x lập thành cấp số cộng ;
A. x = 4, x = 3
B. x = 2, x = 3
C. x = 2, x = 5
D. x = 2, x = 1
Tìm x; y biết: Các số x + 6y; 5x + 2y; 8x + y lập thành cấp số cộng và các số x + 5/3 y, y – 1,2x – 3y lập thành cấp số nhân.
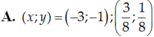
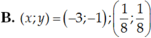
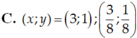
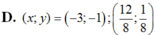
Chọn A.
Ta có hệ: 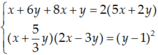
Giải hệ này ta tìm được 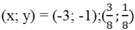
1. tìm x để 3 số 3; 2x + 1; 7 lập thành một cấp số cộng
2. tìm x để 3 số 1; 2x + 1; 9 lập thành một cấp số cộng
1: Để ba số đó lập thành1 cấp số cộng thì
\(\left[{}\begin{matrix}3=2\left(2x+1+7\right)\\2x+1=2\left(3+7\right)=20\\7=2\left(2x+1+3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x+16=3\\x=\dfrac{19}{2}\\2\left(2x+4\right)=7\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{13}{4}\\x=\dfrac{19}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
2: Để ba số này lập thành cấp số cộng thì
\(\left[{}\begin{matrix}1=2\left(2x+1+9\right)\\2x+1=2\left(1+9\right)=20\\9=2\left(1+2x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x+20=1\\x=\dfrac{19}{2}\\4x+4=9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{19}{2}\\x=-\dfrac{19}{4}\\x=\dfrac{5}{4}\end{matrix}\right.\)
Biết rằng 3 số x, y, z lập thành một cấp số nhân và ba số x, 2y, 3z lập thành một cấp số cộng. Tìm công bội của cấp số nhân ?
Ba số x, y, z lập thành một cấp số nhân nên:
y = x.q và z = y.q = x.q2 ( q là công bội)
Ba số x, 2y, 3z lậo thành một cấp số cộng nên:
x + 3z = 4y ⇔ x + 3.(xq2) = 4.(x.q)
⇔ x. (1 + 3q2 – 4q) = 0 ⇔ x = 0 hay 3q2 – 4q + 1 = 0
Nếu x = 0 thì x = y= z= 0, q là một số tùy ý
Nếu x ≠ 0 thì 3q2– 4q + 1 = 0 ⇔\(\Leftrightarrow\left[{}\begin{matrix}q=1\\q=\dfrac{1}{3}\end{matrix}\right.\).
Công bội của cấp số nhân là \(q=1\) hoặc \(q=\dfrac{1}{3}\).
1. Cho 3 số lập thành cấp số cộng. Biết tổng 3 số bằng 6 và tổng bình phương 3 số bằng 30. Tìm các số.
2. Tìm m để phương trình sau có 4 nghiệm lập thành cấp số cộng:
\(x^4-10x^2+9m=0\)
3. Cho cấp số cộng giảm thỏa mãn:
\(\left\{{}\begin{matrix}u_1+u_2+u_3=3\\u_3^2-u_2^2=3\end{matrix}\right.\)
Tính: \(S=\dfrac{1}{u_1u_2}+\dfrac{1}{u_2u_3}+...+\dfrac{1}{u_{19}u_{20}}\)
4. Cho cấp số cộng tăng:
\(\left\{{}\begin{matrix}u_1+u_3+u_5=-3\\u_2+u_4+u_6=3\end{matrix}\right.\)
Tính: \(S=u_1+u_4+u_7+...+u_{88}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn mọi người nhiều!!!
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Tìm các số (x,y) biết y < 0 và các số x+6y, 5x+2y, 8x+y theo thứ tự lập thành cấp số cộng đồng thời các số x+5/3, y -1, 2x – 3y theo thứ tự đó lập thành một cấp số nhân.
A. (3, -1)
B. (-3, -1)
C. (-1,-3)
D. (-1,3)
Ta có hệ phương trình:
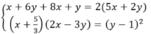
Từ đó ta suy ra
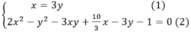
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B
Bài 1: Tìm m để phương trình sau có 3 nghiệm lập thành 1 cấp số cộng:
1, \(x^3-x^2-m^2x+m^2=0\)
2, \((x-2)(x^2-2mx+2m+3)=0\)
3, \(x^3-(2m-3)x^2-mx+m-2=0\)
4, \(x^3+(2m-1)x^2+(4m+1)x+2m+3=0\)
Bài 2: Tìm m để phương trình sau có 4 nghiệm lập thành 1 cấp số cộng:
a, \(-x^4+2mx^2-2m+1=0\)
b, \(x^4+2(m-2)x^2+m^2-5m+5=0\)
Bài 3: Tìm 3 số lập thành 1 cấp số cộng biết tổng của chúng bằng tổng các bình phương bằng 83
Biết x,y, x+4 theo thứ tự lập thành cấp số cộng và x+1, y+1, 2y+2 theo thứ tự lập thành cấp số nhân với x, y là số thực dương. Giá trị của x+y là:
A. 3
B. 2
C. 5
D. 4
Bài 1 : Ba số 5x - y ; 2x + 1 và x - y theo thứ tự lập thành Cấp số cộng . Ba số 3;căn(2x + y) và x + 1 theo thứ tự lập thành Cấp số nhân . Tìm x,y
5x-y;2x+1;x-y lập thành cấp số cộng nên
5x-y+x-y=2(2x+1)
=>6x-2y=4x+2
=>2x-2y=2
=>x-y=1
=>y=x-1
\(3;\sqrt{2x+y};x+1\) lập thành cấp số nhân thì \(\left(\sqrt{2x+y}\right)^2=3\left(x+1\right)\)
=>\(2x+y=3x+3\) hoặc -2x-y=3x+3
=>2x+x-1=3x+3 hoặc -2x-x+1=3x+3
=>-1=3(loại) hoặc -3x+1=3x+3
=>-6x=2
=>x=-1/3
=>y=-1/3-1=-4/3
Thử lại, ta sẽ thấy: 2x+y=-2/3-4/3=-6/3=-2<0
=>\(\sqrt{2x+y}\) không có giá trị
Vậy: Không có cặp số (x,y) nào thỏa mãn đề bài
Tìm x để 3 số : 1-x; x2 ; x+1 theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x
B. x = ± 2 .
C. x = ± 1
D.x=0
Đáp án C
Ba số: 1 − x ; x 2 ; 1 + x lập thành một cấp số cộng khi và chỉ khi:
x 2 = 1 − x + 1 + x 2
⇔ 2 x 2 = 2 ⇔ x = ± 1