Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB
A. E = 5 2 ; 5 2 .
B. E = 3 2 ; − 1 2 .
C. E = − 2 + 3 2 ; 4 + 2 .
D. E = − 2 + 3 2 ; 4 − 2 .
Trong mặt phẳng Oxy cho tam giác đều OAB có cạnh bằng 2, AB song song với Ox, điểm A có hoành độ và tung độ dương
a) Tìm tọa độ hai đỉnh A và B
b) Tìm tọa độ trọng tâm G của tam giác OAB
a) Do AB//Ox và tam giác OAB đều nên điểm A đối xứng với điểm B qua Ox.
Suy ra: AB = 2 = 2b. Nên b = 1.
Áp dụng định lý Pi-ta-go: \(OH=\sqrt{AB^2-HA^2}=\sqrt{2^2-1^2}=\sqrt{3}\).
Suy ra: \(a=\sqrt{3}\Rightarrow x_A=\sqrt{3};y_B=-\sqrt{3}\).
Vậy \(A\left(1;\sqrt{3}\right),B\left(-1;-\sqrt{3}\right)\).
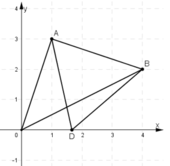
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
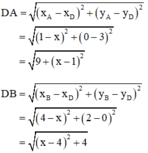
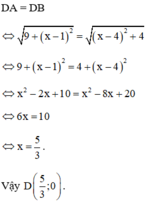
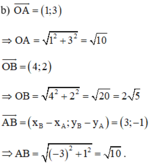
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
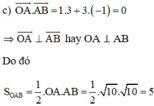
Trong mặt phẳng tọa độ Oxy, xét đường thẳng (d): y = mx + 4 với m≠0.
1. Gọi A là giao điểm của đường thẳng (d) và trục Oy. TÌm tọa độ điểm A.
2. Tìm tất cả các giá trị của m để đường thẳng (d) cắt trục Ox tại điểm B sao cho tam giác OAB là tam giác cân.
Trên mặt phẳng tọa độ Oxy xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA+OB=1 Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
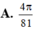
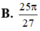
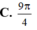
![]()
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
A. 4 π 81
B. 25 π 27
C. 9 π 4
D. 17 π 9
Đáp án A
Khi quay ∆ O A B quanh trục Oy, ta được hình nón có bán kính đáy r = OA và chiều cao h = OB. Theo bài ra, ta có OA + OB = r + h = 1 với (0 < r, h < 1)
Khi đó, thể tích khối nón là V N = 1 3 πr 2 h = 1 3 πr 2 1 - r .
Ta có r 2 1 - r 2 = 4 . r 2 . r 2 . 1 - r ≤ 4 . r 2 + r 2 + 1 - r 3 27 = 4 27 ⇒ V N ≤ 1 3 π . 4 27 = 4 π 81 .
Tham khảo: Ta có thể đưa điểm B có tung độ âm về tung độ dương thì thể tích của khối nón không đổi.
Gọi A a ; 0 B 0 ; b a , b > 0 suy ra phương trình đường thẳng A B : x y + y b = 1 ⇒ x = a - a b . y .
Khi đó V O y = π . ∫ a b a - a b y 2 d y = πa 2 b 3 .
Ta có 4 π 3 . a 2 . a 2 . b ≤ 4 π 3 . a 2 + a 2 + b 3 27 = 4 π 81 ⇒ V M a x = 4 π 81 .
1, Trên mặt phẳng tọa độ Oxy , cho tam giác OAB có A( 0;4 ) ; B(3;0) . Diện tích tam giác OAB là bao nhiêu ???
2. Cho đường thẳng (d) y= 3/4 x+3 cắt 2 trục tọa độ Ox và Oy thứ tự tại A và B . Bán kính đường tròn nội tiếp tam giác AOB ....(đvdt)
trên mặt phẳng tọa độ Oxy,cho điểm A(-2;4) và B(-2;-2).Tính diện tích tam giác OAB ?????? Cứu mìh zới!!!!!!!!!!
Trong mặt phẳng tọa độ oxy,viết phương trình đường thẳng d đi qua điểm M(1,2) và cắt các tia ox,oy lần lượt tại A,B (khác gốc tọa độ O) sao cho tam giác OAB có diện tích bằng 4.
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1