Với vị trí nào của m thì 2 đường thẳng sau đây cắt nhau
△1: 2x-3my+10=0; △2: mx+4y+1=0
xác định vị trí tương đối của 2 đường thẳng sau đây △1: x-2y+1=0; △2: -3x+6y-10=0
21. Cho 4 điểm A(1;2) , B(-1;4) , C(2;2) , D(-3;2) . Tìm.toạ độ giao điểm của hai đg thẳng AB và CD.
31. Với giá trị nào của m hai đg thẳng sau đây sống song
Denta 1: x = 8+(m+1).t ; y = 10 -t
Denta 2: mx +6y -76=0
33. Viết pt tham số của đg thẳng đi qua điểm O(0;0) và song song với đg thẳng Denta : 3x -4y +1=0
41. Với giá trị nào của m thì hai đg thẳng sau đây cắt nhau
Denta 1: 2x -3my +10=0
Denta 2: mx +4y +1=0
21.
\(\overrightarrow{AB}=\left(-2;2\right)=-2\left(1;-1\right)\) nên pt đường thẳng AB:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
\(\overrightarrow{CD}=\left(-5;0\right)=-5\left(1;0\right)\) nên pt CD có dạng:
\(0\left(x-2\right)+1\left(y-2\right)=0\Leftrightarrow y-2=0\)
Giao điểm 2 đường thẳng có tọa độ là nghiệm: \(\left\{{}\begin{matrix}x+y-3=0\\y-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
31.
\(\Delta_1\) nhận \(\left(m+1;-1\right)\) là 1 vtcp
\(\Delta_2\) nhận \(\left(3;-4\right)\) là 1 vtpt
Để hai đường thẳng song song:
\(3\left(m+1\right)+4=0\Rightarrow m=-\frac{7}{3}\)
33.
Đường thẳng d song song \(\Delta\) nên nhận \(\left(3;-4\right)\) là 1 vtpt
\(\Rightarrow\) Nhận \(\left(4;3\right)\) là 1 vtcp
Phương trình tham số: \(\left\{{}\begin{matrix}x=4t\\y=3t\end{matrix}\right.\)
41.
\(\Delta_1\) nhận \(\left(2;-3m\right)\) là 1 vtpt
\(\Delta_2\) nhận \(\left(m;4\right)\) là 1 vtpt
Để 2 đường thẳng cắt nhau
\(\Leftrightarrow2.4\ne-3m^2\Leftrightarrow m^2\ne-\frac{8}{3}\) (luôn đúng)
Vậy hai đường thẳng cắt nhau với mọi m
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
![]()
![]()
![]()
![]()
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: 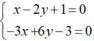 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: 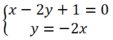 có nghiệm duy nhất (-1/5; 2/5) nên
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 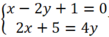 vô nghiệm
vô nghiệm
Vậy Δ // d3
1. Cho hai hàm số bậc nhất y=3x−k+1 và y=mx+k. Tìm điều kiện đối với m và k để đồ thị của hai hàm số là hai đường thẳng trùng nhau.
2. Hai đường thẳng y = 2x và y = 2x+1 có vị trí :
3. Hai đường thẳng y = x+2 và y = 0,5x – 1 có vị trí :
4. Hai đường thẳng y = 1 – 5x và y – 1= – 5x có vị trí :
5. Cho hàm số y=ax+5. Để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là √5 thì hệ số a bằng :
2: Hai đường thẳng này song song
Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?
\({\Delta _1}:mx - y + 1 = 0\) và \({\Delta _2}:2x - y + 3 = 0\).
Vecto pháp tuyến của là: \(\overrightarrow {{n_1}} = \left( {m; - 1} \right)\)
Vecto pháp tuyến của là: \(\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Vậy ai đường thẳng \({\Delta _1}\),\({\Delta _2}\) vuông góc với nhau khi và chỉ khỉ \(\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} \) vuông góc với nhau tức là \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow 2m + 1 = 0 \Leftrightarrow m = \frac{{ - 1}}{2}\)
Bài 2. Với những giá trị nào của m thì đường thẳng y=2x-1 và đường thẳng y=3x+m cắt nhau tại một điểm trên: a) Trục hoành? b) Trục tung?
a) Thay y=0 vào y=2x-1, ta được:
2x-1=0
hay \(x=\dfrac{1}{2}\)
Thay \(x=\dfrac{1}{2}\) và y=0 vào y=3x+m, ta được:
\(m+\dfrac{3}{2}=0\)
hay \(m=-\dfrac{3}{2}\)
Với giá trị nào của m thì hai đường thẳng (∆1) : 2x- 3y - m= 0 và ( ∆ 2 ) : x = 2 = 2 t y = 1 + m t trùng nhau?
A. Không có m
B.m= -2
C. m = 4/3
D.m= 1
Đáp án A
Gọi M( 2+2t; 1+ mt) là điểm tùy ý thuộc ∆2
Để M nằm trên ∆1 khi và chi khi:
2( 2+ 2t) -3( 1+ mt) - m= 0 hay t( 4-3m) + 1- m= 0 n(*) luôn đúng với mọi t.
∆ 1 ≡ ∆ 2 ⇔ ( * ) thỏa với mọi t ⇔ 4 - 3 m = 0 1 - m = 0 (vô nghiệm)
Vậy không có m thỏa yêu cầu bài toán.
1.a) Với giá trị nào của m thì hai đường thẳng y= 2x + 3 + m và y= 3x + 5 - m, cắt nhau tại một điểm trên trục tung
b) Viết phương trình đường thẳng (d) biết (d) song song với (d'): y = \(\dfrac{-1}{2}x\) và cắt trục hoành tại điểm có hoành độ bằng 10
2. Cho các đường thẳng (d1): y= 4mx - (m + 5) với (m\(\ne\)0)
(d2): y= (3m + 1) x + (m - 9)
a) Với giá trị nào của m thì ( d1) // (d2)
b) Với giá trị nào của m thì (d1) cắt (d2). Tìm tọa độ giao điểm khi m = 2
Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)